باورکردنی نیست اما در سال 1202 لئوناردو فیبوناچی توانست به یک سری از اعداد دست پیدا کند که بعدها بعنوان پایه برای بسیاری از رابطههای فیزیک و ریاضی استفاده شد، کافی است از عدد صفر و یک شروع کنید. آنها را کنار هم بگذارید و عدد بعدی را از جمع کردن دو عدد قبل بدست آورید، بسادگی به این رشته از اعداد خواهید رسید :
0,1,1,2,3,5,8,13,21,34,55,89,144, ...
البته برخی از ریاضیدانان عدد صفر را جزو رشته فیبوناچی نمیدانند و یا حداقل آنرا جمله صفرم سری میدانند. نکتهای که تعجببرانگیز است آنکه اگر از عدد سوم نسبت اعداد این سری را به عدد قبلی حساب کنیم خواهیم داشت :
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89
: و یا
1, 2, 1.5, 1,666, 1.6, 1,625, 1.6153, 1.6190, 1.6176, 1.6181, 1.6179 و ...
بله بنظر میرسد که این رشته به سمت همان عدد طلایی معروف میل میکند. بگونهای که اگر نرخ عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد 1.618033988749895 میرسیم که با تقریب 14 رقم اعشار نسبت طلایی را نشان میدهد.
بعدها محاسبات و استدلالهای ریاضی نشان داد که این سری همگرا به سمت نسبت طلایی میباشد و جمله عمومی آنرا با به تقریب میتوان اینگونه نمایش داد :
fn = Phi n / 51/2
که در آن Phi عدد طلایی میباشد. البته فرمولهای دقیق دیگری وجود دارند که اعداد سری و یا اعداد بعدی (Successor) این سری را نمایش میدهند که دراین مطلب به آن نخواهیم پرداخت.
معمای زاد و ولد خرگوش !
در واقع فیبوناچی در سال ۱۲۰۲ به مسئله عجیبی علاقمند شد. او میخواست بداند اگر یک جفت خرگوش نر و ماده داشته باشد و رفتاری برای زاد و ولد آنها تعریف کند در نهایت نتیجه چگونه خواهد شد. فرضیات اینگونه بود :
- شما یک جفت خرگوش نر و ماده دارید که همین الآن بدنیا آمدهاند.
- خرگوشها پس از یک ماه بالغ میشوند.
- دوران بارداری خرگوشها یک ماه است.
- هنگامی که خرگوش ماده به سن بلوغ می رسد حتما" باردار میشود.
- در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده بدنیا میآورد.
- خرگوشها هرگز نمیمیرند.
حال سئوال اینجاست که پس از گذشت یکسال چه تعداد خرگوش نر و چه تعداد خرگوش ماده خواهیم داشت؟ (پاسخ را شما بدهید)
دنباله فیبوناچی در طبیعت
زنبورها
شاید مسأله تولیدمثل خرگوشها کاملاً غیرواقعی باشد ولی اعداد فیبوناتچی برای تولیدمثل زنبورها کامل صدق میکنند. ابتدا باید نکات زیر را در مورد تولید مثل زنبورها بدانید:
- در کلونی زنبورها یک زنبور ملکه وجود دارد که تخم میگذارد.
- سایر زنبورهای ماده کارگر هستند و تخم نمیگذارند. این زنبورها از تخمهای بارور زاده میشوند. یعنی زنبورهای ماده دارای دو والد هستند. زنبور ملکه هم یکی از همین زنبورهای ماده است.
- تعدادی از زنبورها نر هستند که برای تولیدمثل استفاده میشوند. این زنبورهای حاصل تخمهای غیربارور زنبور ملکه هستند. یعنی زنبورهای نر یک والد دارند.
حال بیاییم تعداد اجداد یک زنبور نر را بشمریم. زنبور نر از یک زنبور ملکه متولد شده پس ۱ مادر داشته است. این مادر خود از یک نر و ماده متولد شده. پس زنبور نر اولیه دارای ۲ پدر/مادر بزرگ است. پدربزرگ زنبور نر اولیه یک مادر داشته و مادربزرگ زنبور نر اولیه دو مادر/پدر بزرگ داشته. پس تعداد اجداد زنبور نر اولیه برابر با ۳ است. همین طور که حساب کنید، دنباله اعداد فیبوناتچی به دست میآید.
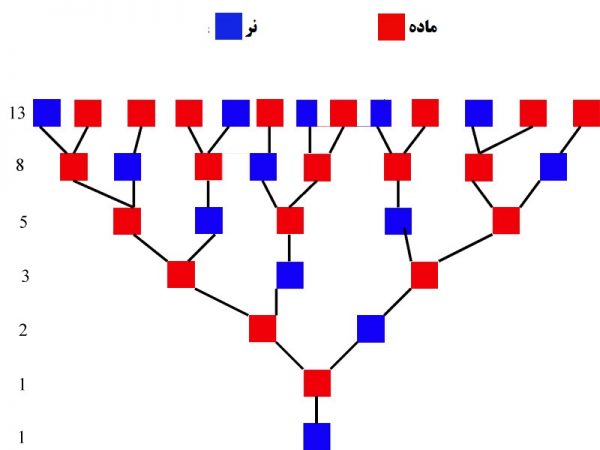
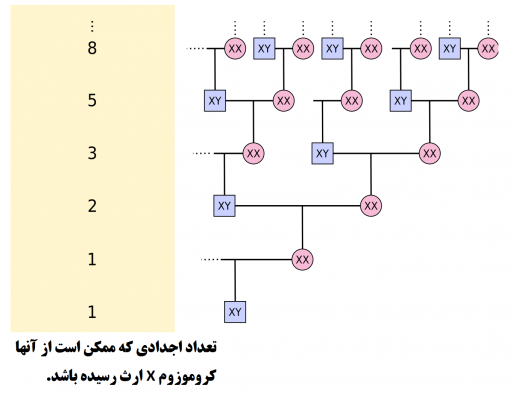
این مسأله برای تعداد اجداد یک انسان مرد که کروموزوم X از آنها به ارث رسیده است هم صدق میکند. میدانیم که کروموزوم X از طریق مادر و Y از طریق پدر به ارث میرسد. شکل زیر این مطلب را برای کروموزوم X نشان میدهد.
گلها و شاخهها
برخی از گیاهان در تعداد شاخههای منشعب شده، تابع اعداد فیبوناتچی هستند. برای مثال گیاه بومادران عطسهآور، در هر دو ماه شاخههای جدید میزند. شکل زیر تعداد شاخهها را در پایان هر دو ماه نشان میدهد.

تعداد گلبرگهای در بسیاری از گیاهان، یکی از اعداد دنباله فیبوناتچی است. یعنی گل بعد از باز شدن دارای مثلاً ۸ گلبرگ یا ۱۳ گلبرگ است. شکلهای زیر این موضوع را به خوبی نشان میدهند.
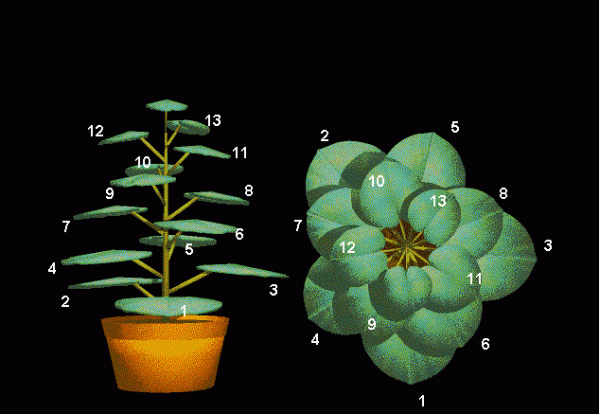
در چینش برگهای بسیاری از گیاهان، دنباله فیبوناچی دیده میشود. چینش برگها باید طوری باشد که برگهای بالایی مانع رسیدن نور به برگهای پایینی نشوند. اگر از پایین شروع به شمردن برگها به دور ساقه کنیم، در هر بار چرخش به دور ساقه، تعداد برگها به یکی از اعداد فیبوناچی میرسد. شکل زیر این موضوع را به خوبی نمایش میدهد.
اعداد فیبوناچی و بدن انسان
خوب در آینه به خودتان نگاه کنید. متوجه میشوید که بیشتر اعضای بدن شما یکی، دوتایی، سه تایی و ... است. شما یک بینی، دو چشم، سه اندام حرکتی و پنج انگشت در هر دست دارید. تناسب و اندازهها بدن انسان را میتوان طوری بر هم تقسیم کرد که به نسبت طلایی رسید. مولکولهای DNA از این دنباله پیروی میکنند؛ هر چرخه مارپیچ دوگانه 34 انگستروم طویل و 21 34 انگستروم عریض دارد.
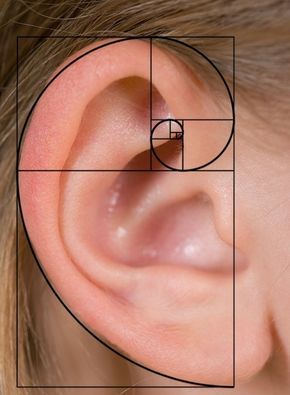
چرا در بسیاری از الگوهای طبیعی میتوان اثری از اعداد فیبوناچی و نسبت طلایی پیدا کرد؟
قرن هاست که دانشمندان به دنبال جواب این سوال هستند. در برخی از موارد این همبستگی فقط یک تصادف است اما در برخی از موارد هم وجود این دنباله و اعداد بخاطر تکامل یک الگوی رشدی مشخص است. در برخی از گیاهان بروز این همبستگی بخاطر قرار گرفتن در معرض نور شدید اتفاق میافتد.
مارپیچ فیبوناچی
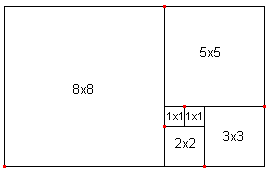
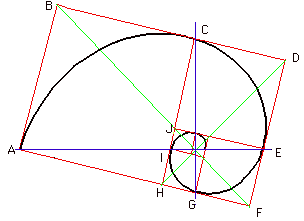
به شکل زیر نگاه کنید و ببینید که به چه زیبایی از کنار هم قرار دادن تعدادی مربع میتوان رشته فیبوناچی را بصورت هندسی نمایش داد. حال اگر در هر یک از این مربعها از نقاط قرمز ربع دایرههایی رسم کنیم در نهایت به نوعی از مارپیچ حلزونی شکل میرسیم که به مارپیچ فیبوناچی (Fibonacci Spiral) معروف میباشد.
مثلا مربعهای یک و یک مربع دو را میسازند؛ مربعهای پنج و هشت مربع ۱۳ را ایجاد میکنند؛ مربعهای هشت و ۱۳ مربع ۲۱ را میسازند و به همین منوال ادامه مییابد. سپس اگر بهاندازهی طول ضلع مربعها کمانهایی رسم شود، در نهایت یک مارپیچ بدست میآید که بهسرعت رشد میکند. بدیهی است که نرخ رشد و باز شدن این مارپیچ متناسب با نرخ بزرگ شدن اعداد در سری فیبوناچی می باشد.
سری فیبوناچی چه در ریاضیات چه در فیزیک و علوم طبیعی کاربردهای بسیار دیگری دارد، ارتباط زیبای فاصله های خوش صدا در موسیقی، چگونگی تولد یک کهکشان و ...
چرا این دنباله اعداد مشهور شده است؟
سری فیبوناچی رشتهای از اعداد است که در آن اعداد غیر از دو عدد اول با محاسبه مجموع دو عدد قبلی ایجاد میشوند.
با وجود گستردگی طبیعت و وجود انواع موجودات پیرامون انسانها، نظم خاصی بر همهچیز حاکم است که با پیشرفت علوم بشری، این نظم بیشازپیش مشخصتر میشود. شاید در زمان یادگیری مفاهیم علمی، بسیاری از موارد بیمعنی به نظر برسد، اما نظم خاصی در پشت همهچیز نهفته است.
ریاضیات یکی از علوم پایه است که کشف اسرار آن، کلید حل معمای موجود در طبیعت است.
همانطور که اشاره شد این اعداد در هستی کشف شدهاند. در قسمت لاک حلزون از زاویه «فی» استفاده شده است. شاخ و برگ درختها بهصورت تصادفی در جهات مختلف رشد نمیکنند. اندازهگیری زاویه شاخهها نشان میدهد که در الگوی رشد آنها، نظمی شبیه دنباله فیبوناچی و نسبت طلایی وجود دارد. درختان با پیروی از این نوع الگوی رشد، قادر هستند درصد بیشتری از نور خورشید را جذب کنند.

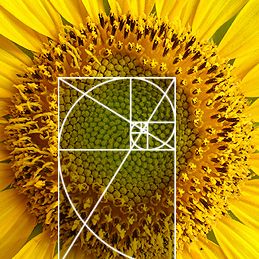
دانههای آفتابگردان به شکل مارپیچهایی روبروی هم رشد میکنند. طبق تحقیقات انجام شده نسبت قطر هر مارپیچ به مارپیچ بعدی ۱.۶۱۸ است.
کاربرد در تحلیل تکنیکال سهام
حال که با مفهوم سری اعداد فیبوناچی آشنا شدید، لازم است با کاربرد آن در تحلیل تکنیکال بازار سهام آشنا شوید. امروزه برای معاملهگران این موضوع اهمیت دارد که بفهمند چگونه این اعداد وارد بازی سهام میشوند و نقش خود را در بازار بر عهده میگیرند.
در ابتدای ایجاد یک بازار، منطقی است که بگوییم کاری که در بازارها انجام میشود، بسیار ساده است. افراد با خرید و فروشهای خود یک بازار را به وجود میآورند؛ اما بهتدریج پیچیدگی بازارها افزایش مییابد. در حال حاضر بسیاری از خبرگان بازار سهام چیزی را نمیخرند، به دلیل اینکه «احساس میکنند آن را دوست دارند یا ندارند». اکنون تحلیلگران تکنیکال سعی میکنند سریع و دقیقتر به این نکته پیببرند که در چه نقطهای از نمودار باید وارد و در چه نقطهای از آن خارج شد.
درصورتیکه به پیچیدگی بازار اعتقاد داشته باشیم، منطقی است که بیشتر معاملهگران در آیندهای نزدیک بهطرف روشهای علمیتر برای معاملات خود سوق پیدا کنند. قبول اهمیت نقاط فیبوناچی توسط معاملهگران درنهایت بهجایی ختم میشود که هرگاه نمودار به سمت این نقاط حرکت میکند، معاملهگران بتوانند رفتار آن را پیشگویی کنند.
با این تفاسیر میتوان گفت که انواع ابزارهای فیبوناچی در بازارهای مالی، روشی برای تحلیل بازگشت یا ادامه روند هستند. از منظری انواع ابزارهای فیبوناچی نقاط حمایت و مقاومت هستند که با ابزارها و روشهای گوناگون رسم میشوند.
این سطوح بازگشت برخلاف حمایت و مقاومتهای قبلی که تنها قیمتی خاص را نقطه حساس تلقی میکردند میتوانند قیمتی خاص، خطی مورب یا زمان خاصی را نقطه حساس حمایت یا مقاومت تعریف کنند. در استفاده از ابزارهای فیبوناچی درصدها اهمیتی فوقالعاده دارند.
عموم این درصدها از نسبت درصدهای بین اعداد فیبوناچی به دست میآیند. بهغیراز چند عدد ابتدای سری اعداد فیبوناچی، هرکدام از اعداد دنباله، تقریبا ۱٫۶۱۸ برابر عدد قبل از خود هستند(نسبت طلایی) و هر عدد ۰٫۶۱۸ برابر عدد بعد از خود است.
این نسبتها به درصد به ترتیب ۱۶۱٫۸ درصد و ۶۱٫۸ درصد میشوند. درصدهای دیگری نیز مهم هستند که در ادامه میآید. تقسیم عدد اول به عدد دوم سری اعداد فیبوناچی یکبهیک یا به عبارتی ۱۰۰ درصد را نشان میدهد.
تقسیم عدد دوم به عدد سوم سری اعداد فیبوناچی ۰٫۵ یا بهعبارتی ۵۰ درصد را نشان میدهد.
در اعداد بالاتر سری اعداد فیبوناچی و تقسیم هر عدد به دو عدد بعد از آن، مشاهده میشود حاصل تقسیم به ۳۸٫۲ درصد تمایل میکند. در اعداد بالاتر سری اعداد فیبوناچی و تقسیم هر عدد به سه عدد بعد از آن، مشاهده میشود حاصل تقسیم به ۲۳٫۶ درصد تمایل دارد.
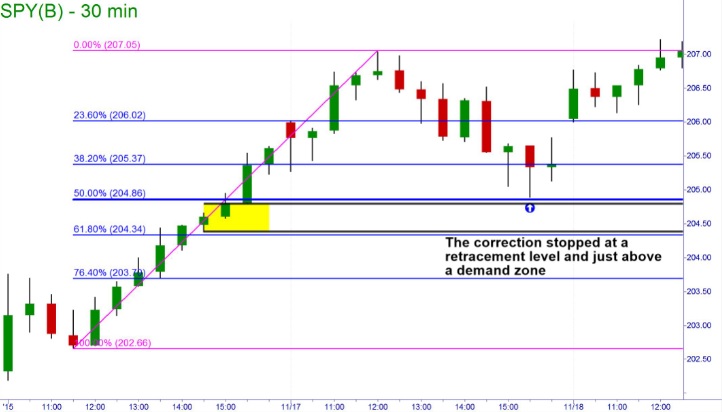
نمودار زیر نشان میدهد که روند قیمتی در بازگشت و تصحیح در محدودههای ۲۳.۶ درصد، ۳۸.۲ درصد و ۵۰ درصد واکنش نشان داده است.
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
![]()





