بینهایت مفهومی است که در رشته‌های مختلف ریاضیات (با تعبیرات مختلف) به‌کار می‌رود و معمولاً به معنای «فراتر از هر مقدار» است. معمولاً نشانه بینهایت در ریاضیات ∞ است. بی نهایت از واژه لاتین finites به معنی محدود گرفته شده ( علامت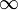 
) چیزی است که "محدود" نیست، که در آن هیچ محدودیت فضایی و زمانی وجود ندارد.
در آنالیز حقیقی بینهایت به معنای حدی بیکران است.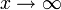 
یعنی متغیر x فراتر از هر مقدار در نظرگرفته شده رشد می‌کند.
در آنالیز مختلط نیز همین علامت با همین نام به‌کار می‌رود. در این رشته یعنی قدر متغیر مختلط x (که آن را با |x| نشان می‌دهند) بیش از هر مقدار در نظر گرفته شده رشد می‌کند.
در نظریه مجموعه‌ها مفهوم بینهایت با اعداد ترتیبی و اعداد اصلی مربوط است. عدد اصلی مجموعه اعداد طبیعی را با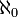 
نمایش می‌دهند و می‌خوانند «الف صفر» (از اولین حرف الفبای عبری به‌نام «الف»). این عدد «تعداد» عددهای مجموعه اعداد طبیعی را نشان می‌دهد، که «بینهایت» است. جالب است که بدانید که عدد اصلی مجموعه‌های N و Z و Q یکسان هستند ولی عدد اصلی مجموعه R برابر عددی است که آن را الف می‌خوانند. خوب است بدانید که الف برابر دو به توان الف صفر می‌باشد. بینهایت دارای دو مفهوم فیزیکی و ریاضی است که کاملاً با یکدیگر متفاوتند.
مفهوم فیزیکی
مفهوم فیزیکی بینهایت، دارای تعریف دقیقی نیست و در جای‌های مختلف دارای تعاریف متفاوت است. به عنوان مثال، می‌گوییم که اگر جسم در کانون عدسی محدب قرار گیرد، تصویر در بینهایت تشکیل می‌شود. حال دو عدسی با فواصل کانونی متفاوت در نظر بگیرید و اجسامی را روی کانون این دو عدسی قرار دهید. طبق قاعده، تصاویر هر دو در بینهایت تشکیل می‌شود. اما قطعا تصویر این دو دقیقا در یک نقطه تشکیل نمی‌شود؛ یعنی بینهایت برای این دو عدسی متفاوت است.
به عنوان مثالی دیگر، دو منبع گرمایی، مثلاً دو اتو با درجه حرارتهای متفاوت را در نظر بگیرید. فاصله‌ای که در آن، دیگر اصلاً گرمای اتو را احساس نکنیم، برای این دو اتو متفاوت است، به عبارت دیگر، بینهایت برای این دو اتو تفاوت دارد.
مفهوم ریاضی
اما مفهوم بینهایت، در ریاضیات کاملاً متفاوت با بینهایت فیزیکی است. علامت بینهایت در ریاضیات، است. در ریاضیات می‌گوییم: «بینهایت مقداری است که از هر مقدار دیگر بیشتر است.» به عنوان مثال، بینهایت را در اعداد طبیعی در نظر می‌گیریم و می‌گوییم: بینهایت از ۱، ۱۰، ۱۰۰، ۱۰۰۰۰۰۰۰۰۰۰ و هر عدد دیگر که در نظر بگیرید، بزرگتر است.
این مفهوم، دقیقا همان مفهومی است که در «حد در بینهایت» در نظر گرفته می‌شود. به عنوان مثال، در تابع، وقتی می‌گوییم، یعنی این که x از هر عدد انتخاب شده بزرگتر است.
یکی از مهم‌ترین مباحثی که بینهایت در آن دارای کاربرد است، نظریه مجموعه هاست. به عنوان مثال می‌دانیم که تعداد اعضای مجموعه اعداد حقیقی و مجموعه اعداد صحیح و طبیعی و ... بینهایت است. (تعداد اعضای هر مجموعه را عدد اصلی می‌نامند) در ریاضیات پیشرفته ثابت می‌شود که عدد اصلی مجموعه اعداد حقیقی و صحیح با یکدیگر برابر نیست.
نگرش باستانی
نگرش باستانی از ارسطو آغاز شده است :
"تفکر درباره یک عدد بزرگ همیشه ممکن است: چون تعداد دفعاتی که می‌توان یک مقدار را به دو نیمه تقسیم کرد، بینهایت است. بنابراین بینهایت، امکان بالقوهای است که هرگز بالفعل نمی‌گردد؛ تعداد اجزایی را که می‌توان به دست آورد، همیشه از هر عدد معینی بیشتر است."
به این مورد اغلب بینهایت "بالقوه" اطلاق می‌شود، بهرحال دو نظریه در این مورد با هم ترکیب شده‌اند. یکی اینکه همیشه پیدا کردن چیزی هایی که تعداد آنها از هر عددی بیشتر باشد ممکن است، اگرچه آن چیزها عملا وجود نداشته باشند. دیگر اینکه ما می‌توانیم بدون محدودیتی، اعداد بالاتر از محدود را شمارش کنیم.
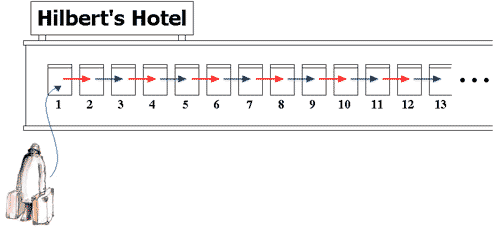
هتل هیلبرت (هتل بی‌نهایتی)
نزدیک به آغاز قرن بیستم، یک ریاضیدان آلمانی دیگر به نام «دیوید هیلبرت» این واقعیت غیر عاید را به صورتی به تصویر کشید که تنها با بینهایت امکان این کار وجود دارد. ریاضیدانان هم اکنون مفهوم "هتل هیلبرت" را به کار می‌برند، مهمانخانه‌ای که تعداد اتاق‌های آن برابر الف- صفر است و بنابراین هرگز اتاق خالی کم نمی‌آورد. حتی اگر تمام اتاق‌های هتل هیلبرت را پر کرده باشند، صاحب هتل هنوز هم می‌تواند برای چند مسافر تازه‌ای که از راه رسیده‌اند اتاق خالی پیدا کند، زیرا بینهایت به اضافه کمی بیشتر هنوز هم بینهایت است که برابر است با تعداد اتاق‌های موجود در مهمانخانه.
در حقیقت، حتی اگر با وجود پر بودن تمام اتاق‌های مهمانخانه باز هم ناگهان سروکله بینهایت مسافر دیگر پیدا شود، هر یک از آنها می‌توانند برای گذراندن شب خود یک اتاق خالی پیدا کنند، چون بینهایت به علاوه بینهایت باز هم بینهایت است.
از نگاه اقلیدس
اصل موضوع اقلیدس:
هر کل از هر جزء خود، اکیدا بزرگتر است.
اگرچه در دنیای طبیعی این اصل درست است، اما پس از ظهور مفهوم مجموعه، مثال‌های نقضی برای آن پیدا شد. مثلاً واضح است که تعداد اعداد طبیعی با تعداد اعداد زوج طبیعی برابر است (کافی است هر عدد طبیعی را با دو برابرش متناظر کنیم)، در حالی که اعداد زوج طبیعی، جزیی از همه اعداد طبیعی هستند.
البته این نکته را نباید فراموش کرد که: مجموعه اعداد طبیعی یک کل می‌باشد که با کل اعداد زوج طبیعی مطابق است اما مفهوم اعداد طبیعی یک کلی است که همواره بیشتر از مفهوم کلی اعداد زوج طبیعی است و منظور از بیشتر به لفظ دقیق‌تر پیشتر می‌باشد که در تصور مفهوم دوم یعنی اعداد زوج به مفهوم اول نیاز است و عکس این قضیه صحیح نیست. در جمع‌بندی باید گفت: مجموعه اعداد طبیعی با مجموعه هر عددی حتی یک برابر است؛ زیرا با فرمولی که با هر متغیر ورودی تغییر می‌کند همواره به عدد ثابتی خواهیم رسید که مثلا می‌توان گفت: مجموع اعدا طبیعی به ازای هر عدد خود یک عدد یک دارد. و البته بودن یا نبودن مصداق برای مفاهیم عام با فلسفه محض است و نه با ریاضیات چنانکه بودن یا نبودن عدد و مقدار با فلسفه است و نه با ریاضی.
از نگاه ددکیند
اشتباه بودن اصل موضوع اقلیدس در زمینه ریاضیات مورد بحث بود، تا این که «ریچارد ددکیند» تعریفی از مفهوم بینهایت ارائه داد. ددکیند هر چیزی را که اصل موضوع اقلیدس برای آن صادق نباشد، بینهایت نامید. پس طبق تعریف ددکیند، بینهایت هر چیزی است که با جزئی از خود هم‌اندازه باشد.
این، شاید اولین تعریف از بینهایت در زمینه نظریه مجموعه باشد. ددکیند مجموعه‌ای را که بینهایت عضو داشته باشد، نامتناهی نامید. پس طبق این تعریف، یک مجموعه را نامتناهی گوییم هرگاه با یک زیرمجموعه سره از خودش هم‌اندازه باشد. مجموعه متناهی، مجموعه‌ایست که نامتناهی نباشد.
از نگاه کانتور
در اواخر قرن نوزده، جورج کانتور به‌طور رسمی نظریه مجموعه را ارائه داد. براساس نظریه کانتور، مجموعه A را k عضوی گوییم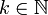 
هرگاه یک تناظر یک به یک بین A و مجموعه 
وجود داشته باشد. مجموعه متناهی مجموعه‌ایست که یا تهی باشد و یا (به ازای یک 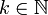،) k عضوی باشد. و بالاخره مجموعه نامتناهی مجموعه‌ایست که متناهی نباشد.
به عبارت دیگر، طبق تعریف کانتور، بینهایت هر چیزی است که نتوان آن را شمرد.
نکته قابل توجه این است که تعریف‌های ددکیند و کانتور از مفهوم بینهایت با هم معادل‌اند؛ به عبارت دیگر، می‌توان نشان داد که یک مجموعه نامتناهی است اگر و تنها اگر با یک زیرمجمموعه سره از خودش هم‌اندازه باشد.
ترا بی نهایت و بینهایت مطلق
اولین و به عبارتی "کوچکترین" بینهایت، بی‌نهایتی است که اغلب ما آن را "بینهایت" تصور می‌کنیم. این بی‌نهایتی است که با شمردن اعداد به سمت بالا و هرگز باز نایستادن به دست می‌آید: ...و۳و۲و۱و۰. و این کار برای همیشه ادامه می‌یابد. کانتور این بینهایت را "الف-صفر" نامید که بخش اول نام آن از اولین حرف الفبای عبری گرفته شده است. تردید نیست که این بینهایت دارای خواصی بسیار عجیب است.
به عنوان مثال، افزودن عدد یک به الف- صفر، یا دو برابر کردن و یا به توان دو رساندن آن، هیچ تاثیری در مقدار آن ندارد و پاسخ همچنان الف- صفر خواهد بود. دلیل این امر آن است وقتی شما با چیزی بینهایت بزرگ سر و کار دارید، هیچ کاری مقدار آن تغییر دهد نمی‌توانید انجام دهید.
اگر با این پاسخ متقاعد نشده‌اید، روی یک ورق کاغذ دو دایره بکشید که قطر یکی دو برابر دیگری باشد. به بیان ریاضی، هر دایره از تعداد بی‌پایانی نقطه تشکیل شده است (زیرا نقطه‌های کوچک کوچکتر می‌شوند)، و محیط دایره برابر با عدد پی ضرب در اندازه قطر آن است. بنابراین محیط دایره بزرگتر دو برابر محیط دایره کوچکتری است که ترسیم کرده‌اند، در حالی که بنابر تعریف، هر دو دایره شامل تعداد بینهایت نقطه‌اند. به عبارت دیگر، دو برابر بینهایت هنوز هم بینهایت است، و حتی بینهایت برابر بینهایت باز همان بینهایت خواهد ماند.
کانتور بی‌نهایت‌های دیگری با خواصی بسیار عجیب تر را نیز یافته بود. "الف- یک" عددی آنچنان بزرگ است که هرگز نمی‌توان به آن رسید، حتی ار شما تا ابد به شمردن ادامه دهید. پس از آن، تعداد بی‌نهایتی از الف‌ها و سار بی‌نهایت‌ها وجود دارند که سرانجام به بی‌نهایتی می‌رسند که همه بی‌نهایت‌های دیگر را زیر چتر خود دارد. کانتور آن را "بینهایت مطلق" نامیده بود. این بینهایت چنان وسیع و بی کران است که اصلا نمی‌توان آن را توصیف کرد. در واقع، تعریف آن بر این اندیشه استوار است که هر تلاشی برای توصیف آن، همواره به توصیف چیزی کوچکتر می‌انجامد.
آخرین یافته‌ها
حدود یک قرن طول کشیده است تا ریاضیدانان روش‌هایی را برای سر و کله زدن با بینهایت بیابند که در میانه راه آنها را به دیوانگی نکشاند. در اوایل دهه 1970، ریاضیدانان انگلیسی «جان کانوی» که هم اکنون در دانشگاه پرینستون حضور دارد، گونه جدیدی از اعداد را موسوم به "اعداد فراواقعی" کشف کرد که علاوه بر تمامی اعداد معمول، اعداد موسوم به ترانهایت و بسیاری از اعداد یر عادی دیگر را نیز شامل می‌شود. در نتیجه این کشف، ریاضیدانان هم اکنون می‌توانند به عنوان مثال، ریشه دوم بینهایت را محاسبه کنند و یا لگاریتم آن را به دست آورند. بدون اینکه به پاسخ‌هایی کاملا بی‌معنا دست یابند.
حتی با این وجود نیز اغلب ریاضیدانان مایلند کاری به کار بینهایت نداشته باشند. بینهایت یک مشکل آفرین واقعی است، که می‌تواند پرسش‌های معقول را به پاسخ‌هایی کاملا بی‌ربط و غیرعادی 0 همچون 1=0 تبدیل کند. اما دانشمندانی که در ماهیت بنیادی عالم کند و کاو می‌کنند، در محاسبات خود مرتب به بینهایت برخورد می‌کنند. معمولا در چنین مواقعی آنها باید تسلیم بینهایت شوند، و یا اینکه برای بیرون راندن بینهایت مزاحم از نتیجه محاسبات خود عذری بتراشند که در نهایت کار جالبی نیست. اما ریاضیدانان برجسته‌ای همچون کانوی و مارتین کروسکال از دانشگاه راتجرز در نیوجرسی، امیدوارند که روزی اعداد فراواقعی دانشمندان را در برخورد با این مسائل مربوط به بینهایت یاری دهند، و به آنها امکان دهند تا پاسخ‌هایی واقعی را برای معماهای عالم بیابند، البته به شرط آنکه کلنجار رفتن با این مسائل آنها را دیوانه نکرده باشد.
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
