هندسه نااقلیدسی-هذلولوی و بیضوی

واژه هندسه عربی شده، واژه «اندازه» در فارسی است. در زبان انگلیسی به آن geometry و در زبان فرانسه به آن géométrie می‌گویند که هردو از γεωμετρία گئومتریا در زبان یونانی آمده است. این کلمه از دو کلمه «جئو» به معنای زمین و «متری» به معنای اندازه‌گیری تشکیل شده است که به معنای اندازه‌گیری زمین است.

تاریخچه هندسه

احتمالا بابلیان و مصریان کهن نخستین کسانی بودند که اصول هندسه را کشف کردند. در مصر هر سال رودخانه نیل طغیان می‌کرد و نواحی اطراف رودخانه را سیل فرا می‌گرفت. این رویداد تمام علایم مرزی میان املاک را از بین می‌برد و لازم می‌شد دوباره هر کس زمین خود را اندازه‌گیری و مرزبندی کند.

مصریان روش علامت‌گذاری زمین‌ها با تیرک و طناب را ابداع کردند. آنها تیرکی را در نقطه‌های مناسب در زمین فرو می‌کردند و تیرک دیگری در جایی دیگر نصب می‌شد و دو تیرک با طنابی که مرز را مشخص می‌ساخت به یکدیگر متصل می‌شدند. با دو تیرک دیگر زمین محصور شده و محلی برای کشت یا ساختمان سازی مشخص می‌شد.

در آغاز هندسه برپایه دانسته‌های تجربی پراکنده‌ای در مورد طول، زاویه، مساحت و حجم قرار داشت که برای ساختمان و نجوم و برخی صنایع دستی لازم می‌شد. بعضی از این دانسته‌ها بسیار پیشرفته بودند. مثلا هم مصریان و هم بابلیان قضیه فیثاغورس را ۱۵۰۰ سال قبل از فیثاغورس میشناختند.

یونانیان دانسته‌های هندسی را مدون کردند و بر پایه‌ای استدلالی قرار دادند. برای آنان هندسه از مهمترین دانش‌ها بود و موضوع آن را مفاهیم مجردی می‌دانستند که اشکال مادی فقط تقریبی از آن مفاهیم مجرد بود. در سال ۶۰۰ قبل از میلاد مسیح، یک آموزگار اهل «ایونیا» (که در روزگار ما بخشی از ترکیه به‌شمار می‌رود) به نام تالس، چند گزاره یا قضیه هندسی را به صورت استدلالی ثابت کرد. او آغازگر هندسه ترسیمی بود. فیثاغورس که او نیز اهل ایونیا و احتمالا از شاگردان تالس بود توانست قضیه‌ای را که به‌نام او مشهور است اثبات کند.

اما دانشمندی به نام اقلیدس که در اسکندریه زندگی می‌کرد، هندسه را به صورت یک علم بیان نمود. وی حدود سال ۳۰۰ پیش از میلاد مسیح، تمام نتایج هندسی را که تا آن زمان شناخته بود، گرد آورد و آنها را به طور منظم، در یک مجموعه ۱۳ جلدی قرار داد. این کتاب‌ها که «اصول هندسه» نام داشتند، به مدت ۲ هزار سال در سراسر دنیا برای مطالعه هندسه به کار می‌رفتند.

براساس این قوانین، هندسه اقلیدسی تکامل یافت. هر چه زمان می‌گذشت، شاخه‌های دیگری از هندسه توسط ریاضیدانان مختلف، توسعه میافت. امروزه در بررسی علم هندسه انواع مختلف این علم را نظیر هندسه تحلیلی و مثلثات، هندسه غیراقلیدسی و هندسه فضایی مطالعه می‌کنیم.

خدمت بزرگی که یونانیان در پیشرفت ریاضیات انجام دادند این بود که آنان احکام ریاضی را به جای تجربه بر استدلال منطقی استوار کردند. قبل از اقلیدس، فیثاغورث و زنون نیز به پیشرفت علم ریاضی خدمت بسیار کرده بودند.

در قرن دوم قبل از میلاد، ریاضیدانی به نام هیپارک، مثلثات را اختراع کرد. وی نخستین کسی بود که تقسیم‌بندی بابلیها را برای پیرامون دایره پذیرفت. به این معنی که دایره را به ۳۶۰ درجه و درجه را به ۶۰ دقیقه و دقیقه را به ۶۰ قسمت برابر تقسیم نمود و جدولی براساس شعاع دایره به دست آورد که وترهای بعضی قوس‌ها را به دست می‌آورد و این قدیمی‌ترین جدول مثلثاتی است که تاکنون شناخته شده است.

بعد از آن دانشمندان هندی موجب پیشرفت علم ریاضی شدند. در سده پنجم میلادی آپاستامبا، در سده ششم، آریابهاتا، در سده هفتم، براهماگوپتا و در سده نهم، بهاسکارا در پیشرفت علم ریاضی بسیار مؤثر بودند.

اصطلاحات بنیادی ریاضیات

طی قرن‌های متمادی ریاضیدانان اشیاء و موضوع‌های مورد مطلعه خود از قبیل نقطه و خط و عدد را همچون کمیت‌هایی در نظرمی‌گرفتند که در نفس خویش وجود دارند. این موجودات همواره همه کوشش‌ها را که برای تعریف و توصیف شایسته آنان انجام می‌شد را با شکست مواجه می‌ساختند. بتدریج این نکته بر ریاضیدانان قرن نوزدهم آشکار گردید که تعیین مفهوم این موجودات نمی‌تواند در داخل ریاضیات معنایی داشته باشد. حتی اگر اصولاً دارای معنایی باشند.

بنابراین، اینکه اعداد، نقطه و خط در واقع چه هستند در علوم ریاضی نه قابل بحث است و نه احتیاجی به این بحث هست. یک وقت برتراند راسل گفته بود که ریاضیات موضوعی است که در آن نه می‌دانیم از چه سخن می‌گوییم و نه می‌دانیم آنچه که می‌گوییم درست است.

دلیل آن این است که برخی از اصطلاحات اولیه نظیر نقطه، خط و صفحه تعریف نشده‌اند و ممکن است به جای آنها اصطلاحات دیگری بگذاریم بی آنکه در درستی نتایج تاثیری داشته باشد. مثلاً می‌توانیم به جای آنکه بگوییم دو نقطه فقط یک خط را مشخص می‌کند، می‌توانیم بگوییم دو آلفا یک بتا را مشخص می‌کند. با وجود تغییری که در اصطلاحات دادیم، باز هم اثبات همه قضایای ما معتبر خواهد ماند، زیرا که دلیل‌های درست به شکل نمودار بسته نیستند، بلکه فقط به اصول موضوع که وضع شده‌اند و قواعد منطق بستگی دارند.

بنابراین، ریاضیات تمرینی است کاملاً صوری برای استخراج برخی نتایج از بعضی مقدمات صوری. ریاضیات احکامی می‌سازند به صورت هرگاه چنین باشد، آنگاه چنان خواهد شد و اساساً در آن صحبتی از معنی فرض‌ها یا راست بودن آنها نیست. این دیدگاه (صوریگرایی) با عقیده کهن‌تری که ریاضیات را حقیقت محض می‌پنداشت و کشف هندسه‌های نااقلیدسی بنای آن را درهم ریخت، جدایی اساسی دارد. این کشف اثر آزادی‌بخشی بر ریاضیدانان داشت.

کلاس‌بندی هندسه

هندسه مقدماتی به دو شاخه تقسیم می‌گردد: 

• هندسه مسطحه
• هندسه فضایی

در هندسه مسطحه، اشکالی مورد مطالعه قرار می‌گیرند که فقط دو بعد دارند، هندسه فضایی، مطالعه اشکال هندسی سه بعدی است. این بخش از هندسه در مورد اشکال سه بعدی چون مکعب‌ها، استوانه‌ها، مخروط‌ها، کره‌ها و غیره است.

در هندسه مدرن شاخه‌های زیر مورد مطالعه قرار می‌گیرند:

• هندسه تحلیلی
  
• هندسه برداری
  
• هندسه دیفرانسیل
  
• هندسه جبری
  
• هندسه محاسباتی
  
• هندسه اعداد صحیح
  
• هندسه اقلیدسی
  
• هندسه نااقلیدسی
  
• هندسه تصویری و ناجابجایی

هندسه اقلیدسی

علومی‌که از یونان باستان توسط اندیشمندان اسلامی محافظت و تکمیل شد، از قرون یازدهم میلادی به بعد به اروپا منتقل شد، بیشتر شامل ریاضی و فلسفه طبیعی بود. فلسفه طبیعی توسط کوپرنیک، برونو، کپلر و گالیله به چالش کشیده شد و از آن میان فیزیک نیوتنی بیرون آمد. چون کلیسا خود را مدافع فلسفه طبیعی یونان می‌دانست و کنکاش در آن با خطرات زیادی همراه بود، اندیشمندان کنجکاو بیشتر به ریاضیات می‌پرداختند، زیرا کلیسا نسبت به آن حساسیت نشان نمی‌داد. بنابراین ریاضیات نسبت به فیزیک از پیشرفت بیشتری برخوردار بود. یکی از شاخه‌های مهم ریاضیات هندسه بود که آن هم در هندسه اقلیدسی خلاصه می‌شد.

در هندسه اقلیدسی یکسری مفاهیم اولیه نظیر خط و نقطه تعریف شده بود و پنچ اصل را به عنوان بدیهیات پذیرفته بودند و سایر قضایا را با استفاده از این اصول استنتاج می‌کردند. اما اصل پنجم چندان بدیهی به نظر نمی‌رسید. بنابر اصل پنجم اقلیدس از یک نقطه خارج از یک خط، یک خط و تنها یک خط می‌توان موازی با خط مفروض رسم کرد. برخی از ریاضیدانان مدعی بودند که این اصل را می‌توان به عنوان یک قضیه ثابت کرد. در این راه بسیاری از ریاضیدانان تلاش زیادی کردند و نتیجه نگرفتند. خیام ضمن جستجوی راهی برای اثبات «اصل توازی» مبتکر مفهوم عمیقی در هندسه شد.

در تلاش برای اثبات این اصل، خیام گزاره‌هایی را بیان کرد که کاملا مطابق گزاره‌هایی بود که چند قرن بعد توسط والیس و ساکری ریاضیدانان اروپایی بیان شد و راه را برای ظهور هندسه‌های نااقلیدسی در قرن نوزدهم هموار کرد. سرانجام و پس از دو هزار سال اصولی متفاوت با آن بیان کردند و هندسه‌های نااقلیدسی شکل گرفت. بدین ترتیب علاوه بر فلسفه طبیعی ریاضیات نیز از انحصار یونانی خارج و در مسیری جدید قرار گرفت و آزاد‌اندیشی در ریاضیات آغاز گردید.

اشکالات وارد بر هندسه اقلیدسی

هندسه اقلیدسی بر اساس ۵ اصل موضوع زیر شکل گرفت:

• اصل اول: از هر نقطه می‌توان خط مستقیمی به هر نقطه دیگر کشید.
• اصل دوم: هر پاره‌خط مستقیم را می‌توان روی همان خط به طور نامحدود امتداد داد.
• اصل سوم: می‌توان دایره‌ای با هر نقطه دلخواه به عنوان مرکز آن و با شعاعی مساوی هر پاره‌خط رسم کرد.
• اصل چهارم: همه زوایای قائمه با هم مساوی‌اند.
• اصل پنجم: از یک نقطه خارج یک خط، یک خط و و تنها یک خط می‌توان موازی با خط مفروض رسم کرد.

اصل پنجم اقلیدس که ایجاز سایر اصول را نداشت، به هیچوجه واجد صفت بدیهی نبود. در واقع این اصل بیشتر به یک قضیه شباهت داشت تا به یک اصل. بنابراین طبیعی بود که لزوم واقعی آن به عنوان یک اصل مورد سوال قرار گیرد. زیرا چنین تصور می‌شد که شاید بتوان آن را به عنوان یک قضیه، نه اصل، از سایر اصول استخراج کرد، یا حداقل به جای آن می‌توان معادل قابل قبول‌تری قرار داد.

در طول تاریخ ریاضیدانان بسیاری از جمله، خواجه نصیرالدین طوسی، جان والیس، لژاندر، فورکوش بویویی و … تلاش کردند اصل پنجم اقلیدس را با استفاده از سایر اصول نتیجه بگیرند و آن را به عنوان یک قضیه اثبات کنند. اما تمام تلاش‌ها بی‌نتیجه بود و در اثبات دچار خطا می‌شدند و به نوعی همین اصل را در اثبات خود به کار می‌بردند. دلامبر این وضع را افتضاح هندسه نامید تا اینکه هندسه نااقلیدسی پا به عرصه وجود نهاد.

پیدایش هندسه نااقلیدسی

همه با نام اقلیدس و کتاب جاودانی او، اصول (Elements) که بحق جزء تاثیرگذارترین و مهمترین کتاب‌های تاریخ بشر قلمداد می‌شود، آشنا هستیم. اقلیدس در این کتاب از تعداد انگشت شماری «اصول موضوع» تعداد نسبتا قابل توجهی «قضیه» نتیجه‌گیری می‌کند. کار عظیم اقلیدس این بود که چند اصل ساده چند حکم که بی‌نیاز به توجیه، پذیرفتنی بودند دست‌چین کرد و از آنها ۴۶۵ گزاره را نتیجه گرفت که بسیاری از آنها پیچیده بودند و به طور شهودی، بدیهی نبودند و تمام اطلاعات زمان او را در برداشتند. یک دلیل بر زیبایی «اصول» اقلیدس این است که این همه را از آن اندک نتیجه گرفته است. در میان پنج اصل موضوع اقلیدس اصل پنجم یا اصل توازی که در بالا بدان اشاره شد، موجب زحمت فکری بود: نه چندان ساده بود که بتوان اصل بودنش را بی‌نگرانی پذیرفت، قابل اثبات هم نبود.

از همان آغاز کسانی دچار دودلی شدند و وقت بسیاری را برای اثبات آن یا قرار دادن اصلی به جای آن صرف کردند. این کوشش‌ها هرچند به نتیجه قطعی نرسیدند، راه را برای رسیدن به نتیجه مهمتری گشودند. در قرن نوزدهم، سه دانشمند، گاوس در آلمان، بولیایی در مجارستان و لوباچفسکی در روسیه تقریبا همزمان به کشف هندسه‌هایی دست یافتند که گاوس بر آنها نام هندسه نااقلیدسی نهاد.

نیکلای ایوانوویچ لوباچفسکی در سال ۱۸۲۹ مقاله‌ای در زمینه هندسه نااقلیدسی منتشر ساخت. هنگامی‌که اثر او منتشر شد چندان مورد توجه قرار نگرفت، بیشتر به این علت که به زبان روسی نوشته شده بود و روس‌هایی که آن را می‌خواندند، سخت خرده‌گیری می‌کردند. وی در سال ۱۸۴۰ مقاله‌ای به زبان آلمانی منتشر کرد که مورد توجه گاوس قرار گرفت. گاوس در نامه‌ای به ه.ک. شوماخر از آن مقاله ستایش کرد و در عین حال تقدم خود را در این زمینه تکرار کرد. لوباچفسکی هندسه‌اش را در آغاز «هندسه انگاری» و بعد «هندسه عام» نام گذارد و موضوع آن را در مقاله‌هایی که منتشر کرد به طور کامل بسط داد.

لوباچفسکی علنا با تعلیمات و اصول عقاید کانت درباره فضا، به مثابه شهود ذهنی، به مبارزه برخاست و در سال ۱۸۳۵ نوشت:

تلاش‌های بی‌ثمری که از زمان اقلیدس تاکنون صورت گرفته است... این بدگمانی را در من برانگیخت که حقیقت... در داده‌ها وجود ندارد و برای اثبات آن مثل مورد قوانین دیگر طبیعت کمک‌های تجربی، مثلا مشاهدات نجومی نیاز است.

اریک تمپل بل در کتاب «مردان ریاضیات» لوباچفسکی را آزادکننده بزرگ دانش هندسه نام داده است. بل می گوید: نام او باید برای هر بچه مدرسه‌ای به اندازه نام‌های میکل آنژ یا ناپلئون آشنا باشد. بدبختانه از لوباچفسکی در دوران حیاتش تجلیل نشد. و در حقیقت در ۱۸۴۶ به رغم بیست سال خدمت برجسته‌ای که با عنوان استاد و رئیس انجام داده بود، از دانشگاه قازان اخراج شد. او مجبور شد در سال پیش از مرگش، به علت نابینایی، آخرین کتابش را تقریر کند تا برایش بنویسند.

انواع هندسه‌های نااقلیدسی

اساساً هندسه نااقلیدسی چیست؟ هر هندسه‌ای غیر از اقلیدسی را نااقلیدسی می‌نامند. از این گونه هندسه‌ها تا به حال زیاد شناخته شده است. اختلاف بین هندسه‌های نااقلیدسی و اقلیدسی تنها در اصل توازی است. در هندسه اقلیدسی به ازای هر خط و هر نقطه ناواقع بر آن یک خط می‌توان موازی با آن رسم کرد.

نقیض این اصل را به دو صورت می‌توان در نظر گرفت. تعداد خطوط موازی که از یک نقطه ناواقع بر آن، می‌توان رسم کرد، بیش از یکی است. و یا اصلاً خطوط موازی وجود ندارند. با توجه به این دو نقیض، هندسه‌های نااقلیدسی را می‌توان به ۲ گروه تقسیم کرد.

هندسه هذلولوی

در هندسه نااقلیدسی، نقیض اصل توازی را به عنوان اصل موضوع مفروض می‌گیریم. یعنی این گزاره را که «از یک نقطه خارج از یک خط راست، بیش از یک نقطه می‌توان به موازات آن رسم کرد» به جای اصل موضوع توازی اقلیدس قرار می‌دهیم. این امر به هندسه حیرت‌انگیزی منجر می‌شود که با هندسه اقلیدسی تفاوت اساسی دارد. به قول گاوس قضایای این هندسه به باطن ما می‌مانند و شاید در نظر فردی مبتدی بی‌معنی جلوه کنند. ولی تفکر پیگیر و آرام آشکار می‌سازد که هیچ چیز ناممکن در آنها نیست، مثلا، سه زاویه مثلث تا بخواهید می‌توانند کوچک شوند به شرطی که اضلاع آن به اندازه کافی بزرگ شوند و تازه اضلاع مثلث هرچه باشند، مساحت مثلث هیچ گاه نمی‌تواند از حد معینی زیادتر شود و در واقع هیچ‌گاه هم نمی‌تواند به آن برسد.

گاوس در نامه تاریخی خود به دوست ریاضیدانش «تاورینوس» می‌گوید:

همه تلاش‌های من برای یافتن یک تناقض یا یک ناسازگاری در این هندسه نااقلیدسی به شکست انجامیده است. چیزی که در آن با ادراک ما مغایرت دارد این است که اگر راست باشد، باید در فضای آن یک اندازه خطی وجود داشته باشد که خود به خود معین است اگر چه ما آن را نمی‌دانیم... هرگاه این هندسه نااقلیدسی راست باشد و بتوان آن مقدار ثابت را با همان کمیاتی که به هنگام اندازه‌گیری‌هایمان بر روی زمین و در آسمان بدان‌ها برمی‌خوریم، مقایسه کنیم آن گاه ممکن است آن مقدار ثابت را پس از تجربه تعیین کرد. در نتیجه، من گاهی به شوخی آرزو کرده‌ام که هندسه اقلیدسی راست نبود، چون در آن صورت ما از پیش‌انگاره مطلقی برای اندازه‌گیری داشتیم.

در هندسه هذلولی می‌توان ثابت کرد که اگر دو مثلث متشابه باشند، آنگاه قابل انطباق‌اند. به عبارت دیگر ملاک «ززز» برای قابلیت انطباق درست است در هندسه هذلولی ممکن نیست مثلثی را بدون انداختن از شکل طبیعی بزرگ یا کوچک کرد. در نتیجه در یک جهان هذلولی، عکاسی ذاتا جنبه فرا واقع‌گرایی سور رئالیستی پیدا خواهد کرد. یک نتیجه تکان‌دهنده قضیه مذکور این است که در هندسه هذلولی یک پاره‌خط می‌تواند به کمک یک زاویه مشخص شود. یعنی یک زاویه از یک مثلث متساوی‌الساقین، طول یک ضلع را به طور منحصر به فرد معین می‌سازد. همان‌طور که در نامه گاوس به تاورینوس نیز ذکر گردید، اغلب با بیان اینکه هندسه هذلولی واحد مطلق طول دارد، این نکته را هیجان‌انگیزتر می‌کنند. اگر هندسه جهان مادی هندسه هذلولی بود لازم نبود واحد طول با دقت در دفتر استانداردها نگهداری شود.

در هندسه اقلیدسی، تقسیم هر زاویه به سه قسمت برابر، به وسیله ستاره خط کش غیرمدرج و پرگار تنها، نشدنی است.

در هندسه هذلولی، علاوه بر آنکه این تقسیم نشدنی است، تقسیم هر پاره‌خط به سه قسمت برابر نیز به وسیله ستاره و پرگار تنها، نشدنی است در هندسه اقلیدسی، رسم چهارضلعی منتظمی که مساحت آن برابر مساحت دایره مفروضی باشد، شدنی نیست ولی در هندسه هذلولی این کار شدنی است.

هندسه بیضوی

 در سال ۱۸۵۴ برنارد ریمان نشان داد که اگر نامتناهی بودن خط مستقیم کنار گذاشته شود و صرفاً بی‌کرانگی آن مورد پذیرش واقع شود، آنگاه با چند جرح و تعدیل جزیی اصول موضوعه دیگر، هندسه سازگار نااقلیدسی دیگری را می‌توان به دست آورد. پس از این تغییرات اصل توازی هندسه بیضوی بصورت زیر ارایه گردید.

اصل توازی هندسه بیضوی: از یک نقطه ناواقع بر یک خط نمی‌توان خطی به موازات خط مفروض رسم کرد.

یعنی در هندسه بیضوی، خطوط موازی وجود ندارد. با تجسم سطح یک کره می‌توان سطحی شبیه سطح بیضوی در نظر گرفت. این سطح کروی را مشابه یک صفحه در نظر می‌گیرند. در اینجا خطوط با دایره‌های عظمیه کره نمایش داده می‌شوند. بنابراین خط ژیودزیک یا مساحتی در هندسه بیضوی بخشی از یک دایره عظیمه است.

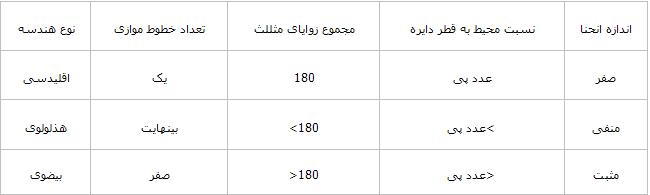
در هندسه بیضوی مجموع زوایای یک مثلث بیشتر از ۱۸۰ درجه است. در هندسه بیضوی با حرکت از یک نقطه و پیمودن یک خط مستقیم در آن صفحه، می‌توان به نقطه اول باز گشت. همچنین می‌توان دید که در هندسه بیضوی نسبت محیط یک دایره به قطر آن همواره کمتر از عدد پی است.

مفهوم و درک شهودی انحنای فضا

سوال اساسی این است که کدام یک از این هندسه‌های اقلیدسی یا نااقلیدسی درست است؟
پاسخ صریح و روشن این است که باید انحنای یک سطح را تعیین کنیم تا مشخص شود کدام یک درست است. بهترین دانشی که می‌تواند در شناخت نوع هندسه یک سطح مورد استفاده و استناد قرار گیرد، فیزیک است. یک صفحه  کاغذ بردارید و در روی آن دو خط متقاطع رسم کنید. سپس انحنای این خطوط را در آن نقطه تعیین کرده و با توجه به تعریف انحنای سطح، حاصلضرب آن را به دست می‌آوریم. اگر مقدار انحنا برابر صفر شد، صفحه اقلیدسی است، اگر منفی شد می‌گوییم صفحه هذلولوی است و در صورتی که مثبت شود، ادعا می‌کنیم که صفحه بیضوی است.

در کارهای معمولی مهندسی نظیر ایجاد ساختمان یا ساختن یک سد بر روی رودخانه، انحنای سطح مورد نظر برابر صفر است، به همین دلیل در طول تاریخ، مهندسین همواره از هندسه اقلیدسی استفاده کرده‌اند و با هیچگونه مشکلی هم مواجه نشدند. یا برای نقشه‌برداری از سطح یک کشور اصول هندسه اقلیدسی را بکار می‌برند و فراز و نشیب نقاط مختلف آن را مشخص می‌کنند. در این محاسبات ما می‌توانیم از خط‌کش‌هایی که در آزمایشگاه یا کارخانه‌ها ساخته می‌شود، استفاده کنیم. حال سوال این است که اگر خط‌کش مورد استفاده ما تحت تاثیر شرایط محیطی قرار بگیرد چه باید کرد؟ اما می‌دانیم از هر ماده‌ای که برای ساختن خط‌کش استفاده کنیم، شرایط فیزیکی محیط بر روی آن اثر می‌گذارد. البته با توجه با تاثیر محیط بر روی خط‌کش ما تلاش می‌کنیم از بهترین ماده ممکن استفاده کنیم. به‌همین دلیل چوب از لاستیک بهتر است و آهن بهتر از چوب است.

اما برای مصافت‌های دور نظیر فواصل نجومی از چه خط‌کشی می‌توانیم استفاده کنیم؟ طبیعی است که در اینجا هیچ خط‌کشی وجود ندارد که بتوانیم با استفاده از آن فاصله بین زمین و ماه یا ستارگان را اندازه بگیریم. بنابراین باید به سایر امکاناتی توجه کنیم که در عمل قابل استفاده است. اما در اینجا چه امکاناتی داریم؟ بهترین ابزار شناخته شده امواج الکترومغناطیسی است. اگر مسیر نور در فضا خط مستقیم باشد، در اینصورت با جرات می‌توانیم ادعا کنیم که فضا، اقلیدسی است. برای پی‌بردن به نوع انحنای فضا باید مسیر پرتو نوری را مورد بررسی قرار دهیم.

اما تجربه نشان می‌دهد که مسیر نور هنگام عبور از کنار ماده، یعنی زمانی که از یک میدان گرانشی عبور می‌کند، خط مستقیم نیست، بلکه منحنی است. بنابراین فضای اطراف اجسام، اقلیدسی نیست. به عبارت دیگر ساختار هندسی فضا، نااقلیدسی است.

انحنای سطح یا انحنای گاوسی

اگر خط را راست فرض کنیم نه خمیده، چنانچه ناگزیر باشیم یک انحنای عددی k به خطی نسبت دهیم برای خط راست خواهیم داشت  k=o انحنای یک دایره به شعاع r برابر است با k=۱/r.

همچنین منحنی هموار، منحنی‌ای است که مماس بر هر نقطه‌اش به بطور پیوسته تغییر کند. به عبارت دیگر منحنی هموار یعنی در تمام نقاطش مشتق‌پذیر باشد.

برای به دست آوردن انحنای یک منحنی در یک نقطه، دایره بوسان آنرا در آن نقطه رسم کرده، انحنای منحنی در آن نقطه برابر با انحنای دایره بوسان در آن نقطه است. دایره بوسان در یک نقطه از منحنی، دایره‌ای است که در آن نقطه با منحنی بیشترین تماس را دارد. توجه شود که برای خط راست شعاع دایره بوسان آن در هر نقطه واقع بر آن بینهایت است.

برای تعیین انحنای یک سطح در یک نقطه، دو خط متقاطع مساحتی در دو جهت اصلی در آن نقطه انتخاب کرده و انحنای این دو خط را در آن نقاط تعیین می‌کنیم. فرض کنیم انحنای این دو خط

k_۱=۱/R_۱ و k_۲=۱/R_۲

باشند. آنگاه انحنای سطح در آن نقطه برابر است با حاصلضرب این دو انحنا، یعنی :

k=۱/R_۱R_۲

انحنای صفحه اقلیدسی صفر است. همچنین انحنای استوانه صفر است:

k=o

برای سطح هذلولوی همواره انحنای سطح منفی است:

k<0

برای سطح بیضوی همواره انحنا مثبت است:

k>0

در جدول زیر  هر سه هندسه با یکدیگر مقایسه شده‌اند:

نتیجه

شاید به نظر برسد که چون ریاضیات، برخلاف علوم طبیعی مثل فیزیک، نجوم و شیمی، با مشاهدات تجربی در تماس نیست؛ هیچگاه با اعوجاج و بحران مواجه نخواهد شد؛ اما همان‌طور که دیدیم، اعوجاج در ریاضیات از نوع دیگری است؛ مثلاً تردید درباره اصل بودن اصل توازی همچون اعوجاجی در هندسه آشکار شد و با مقاومت در برابر کوشش‌های ریاضیدانان جهت اثبات آن، جامعه ریاضیدانان را با بحران مواجه نمود.

اما نکته بسیار مهم این است که این اعوجاج و بحران در پی آن در بنیادی‌ترین سطح هندسه به طرد هندسه اقلیدسی نیانجامید؛ بلکه به مدت بیش از دو هزار سال، تسلط خود را نه تنها بر هندسه، بلکه به علوم دیگر مثل نجوم، فیزیک و حتی فلسفه حفظ نمود. چرا؟ زیرا اگر هندسه‌دانان، هندسه اقلیدسی را به سبب اعوجاجی که در اصول بنیانیاش بود، رها می‌کردند، هیچ نظریه جانشینی نداشتند. در این صورت، تکلیف فعالیت پژوهشی آنها در هندسه چه می‌شد؟ همین تعلقات سبب شد که هندسه اقلیدسی بیش از دو هزار سال تنها پارادایم حاکم در حوزه ریاضیات باشد. زمانی که بویوئی، گاوس و لوباچفسکی هندسه جدید را مطرح کردند، نظریه رقیبی برای هندسه اقلیدسی ظاهر شده بود که می‌توانست جانشین آن شود. همین، موجبات انقلاب نااقلیدسی را فراهم نمود. اما دیدیم که تغییر حمایت از پارادایم اقلیدسی به نااقلیدسی از جانب یکایک ریاضیدانان ناشی از برهان‌های صرفاً منطقی درباره سازگاری هندسی نااقلیدسی نبود؛ زیرا جامعه ریاضی قرن نوزدهم به مدت 26 سال از زمانی که لباچفسکی آن را منتشر کرد تا زمان مرگ گاوس از این برهان‌ها آگاهی داشت، اما هیچ‌گاه آن را جدی نگرفت. آنچه سبب پذیرش هندسه نااقلیدسی شد، عاملی بود ورای استدلال‌های ریاضی و آن اینکه شخصی همچون گاوس شهزاده ریاضیدانان، در نامه‌هایش از آن طرفداری کرده بود. در واقع، ریاضیدانان نیز همچون دانشمندان به دلایل گوناگون طرفدار پارادایم جدید می‌شوند و معمولاً در آن واحد بنابر وجود چند دلیل چنین می‌کنند. بعضی ازاین دلایل -مثلاً خورشیدپرستی- کاملاً در خارج قلمرو آشکار علم قرار دارد. بعضی دیگر وابسته به مزاج شخص و زندگی‌نامه و شخصیت اوست - حتی ملیّت یا شهرت سابق شخص نوآور و استادان وی گاه میتواند نقش مؤثر ایفا کند. شهرت و اعتبار گاوس سبب شد که تعدادی از بهترین ریاضیدانان که مرجعیت جامعه ریاضی به عهده‌شان بود، از هندسه نااقلیدسی حمایت کنند و این سبب پذیرش این هندسه شد. به قول چالمرز (A.F. Chalmers):

انقلاب علمی عبارت است از طرد یک پارادایم و قبول پارادایمی جدید، نه از سوی یک دانشمند به تنهایی؛ بلکه از سوی جامعه علمی مربوطه در تمامیت آن.

بنابراین آنچه توسط استقرارگرایان و ابطال‌گرایان به عنوان منطق اکتشافات علمی گفته می‌شود، باید به‌طور جدی مورد تجدیدنظر قرار گیرد؛ زیرا همان‌طور که دیدیم، عملکرد دانشمندان و حتی ریاضیدانان در رسیدن به نظریه‌های علمی جدید، رفتاری کاملاً بشری است که ما می‌توانیم در حوزه‌های دیگر زندگی‌شان ببینیم. همان‌طور که هری کالینز (Harry Collins) و ترور پینچ (Trevor Pinch) دو جامعه‌شناس علم معاصر، می‌گویند: "آنچه پژوهش‌های موضعی ما نشان می‌دهد، این است که هیچ منطق اکتشاف علمی وجود ندارد و یا بلکه اگر چنین منطقی وجود دارد، آن منطق، منطق زندگی روزمره است "

گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir