زندگی نامه جرج برنارد ریمان

جورج فردریش برنارد ریمان ریاضی‌دان آلمانی که سهم عمده‌ای در آنالیز، نظریه اعداد و هندسه دیفرانسیل داشت و کارهایش در زمینه آنالیز و هندسه دیفرانسیل، پایه ریاضی نظریه نسبیت عام شد. 

در رشته آنالیز حقیقی، او بیشتر به خاطر اولین فرمول‌بندی دقیق انتگرال، انتگرال ریمان و کارش روی سری فوریه شناخته می‌شود. مشارکت‌ و همکاری او در آنالیز مختلط، شامل سطوح ریمانی و زمینه‌های جدید در توضیح طبیعی و هندسی آنالیز مختلط است. مقاله او در سال 1859 در مورد تابع شمارنده اعدا اول، که حاوی بیانیه اصلی حدس ریمان است، به عنوان یک مقاله پایه نظریه  تحلیلی  اعداد در نظر گرفته می‌شود. ریمان از طریق مشارکت‌های پیشگام خود در هندسه دیفرانسیل، پایه های ریاضیات نسبیت عام را بنا نهاد.

بسیاری او را یکی از بزرگترین ریاضیدانان تمام دوران می دانند.

زندگی

این ریاضیدان آلمانی در خانواده‌ای مذهبی و تهیدست به دنیا آمد. پدر او، فردریش برنارد ریمان، یک کشیش بود که در میانسالی با «کارلوت ابل» ازدواج کرد. ریمان دومین فرزند از شش فرزند خانواده بود. پدر وی به عنوان یک کشیش روستایی که در جنگ‌های ناپلئون شرکت داشت سعی فراوان می‌کرد تا خوراک و پوشاک خانواده پر جمعیتش را فراهم کند.

بل در شرح زندگی وی می‌نویسد : وضعیت نامطلوب سلامتی و مرگ زود هنگام بسیاری از فرزندان ریمان بخاطر سوء تغذیه آنها در دوران کودکی بود و ربطی به بنیه ضعیف آنها نداشت. مادر این خانواده نیز قبل از بزرگ شدن فرزندانش از دنیا رفته بود.

ریمان از همان دوران اولیه کودکی صفات مشخصه خود را بروز داد، توانایی محاسباتی شگرف همراه با ترس ذاتی و کم جراتی همیشگی برای صحبت کردن در حضور دیگران. بچه‌ها وی را بخاطر کمرو بودن بیش از حدش مورد تمسخر قرار می‌دادند و این علتی برای پناه بردن بیشتر وی به دنیای کاملا محرمانه ریاضیات می‌شد.

ریمان شدیدا به خانواده خود علاقه داشت و این علاقه وی را وا می‌داشت تا با به خطر انداختن سلامتی خود و فقری که گریبانگیرشان بود برای والدین و بخصوص خواهران محبوبش هدایایی تهیه کند. وی برای رضایت خاطر پدرش تصمیم گرفت که در رشته الهیات تحصیل کند.

هدف وی این بود که هر چه زودتر بتواند به عنوان یک کشیش در آمدی کسب کرده و به وضعیت مالی خانواده‌اش سرو سامانی بدهد.

دوران تحصیل ریمان

برنارد در سال 1840 مستقیما وارد کلاس سوم در لیکوم (Lyceum) هانوفر  شد. تا زمانی که در لیکوم تحصیل می‌کرد با مادر بزرگش زندگی می‌کرد تا اینکه مادربزرگش در سال 1842 در گذشت و به عنوان دانشجوی سال آخر به لونبرگ (Luneburg) منتقل شد. به نظر می‌رسید برنارد دانش آموز خوب و نه ممتاز و در موضوعات کلاسیک مانند زبان عبری و الهیات سخت کوش بوده است. او علاقه ویژه‌ای به ریاضیات نشان داد و سرپرست دبیرستان به او اجازه داد که متون ریاضی را در کتابخانه‌اش مطالعه کند. در فرصتی مناسب او کتاب لژاندر (Legendre) را که درباره‌ی نظریه اعداد بود به برنارد قرض داد و برنارد این کتاب 900 صفحه‌ای را در مدت 6 روز خواند.

ریمان در بهار سال 1846 در دانشگاه گوتینگن (Gottingen) ثبت نام کرد. پدرش او را به تحصیل الهیات تشویق کرد و بنابراین او وارد دانشکده الهیات شد. با این وجود او در برخی از کلاسهای ریاضیات حضور یافت و از پدرش خواست که آیا می‌تواند برای خواندن ریاضیات به دانشکده  فلسفه برود. جایی که ریمان برای اولین بار کارل فردریک گائوس «پادشاه ریاضیدانان» یکی از بزرگترین ریاضیدانان تمام دوران تاریخ را ملاقات نمود.

حتی اگر امروز هم شما از هر ریاضیدانی بخواهید تا سه نفر از معروفترین ریاضیدانان در طول تاریخ را نام ببرد بی شک نام ارشمیدس، ایزاک نیوتن و کارل گائوس را خواهد برد.

به نظر می رسد برنارد جایگاه مناسبی در گوتینگن برای مطالعه ریاضیات دارد، اما در آن زمان دانشگاه گوتینگن جایگاه نسبتا پایینی در ریاضیات داشت. با این که گاوس دبیر ریمان بود اما تنها دوره مقدماتی را به او یاد داد و هیچ دلیلی وجود نداشت که در این مدت به نبوغ ریمان در ریاضیات پی ببرد. با این وجود مطمئنا استرن پی برده بود که دانش آموز ممتازی دارد زیرا که بعدها در وصف ریمان چنین گفته است :

... «... تا کنون همچون قناری نغمه سرایی کرده است. »...

ریمان در بهار 1847 از گوتینگن به دانشگاه برلین (Berlin University) رفت تا زیر نظر اساتیدی چون استینر (Steiner)، ژاکوبی (Jacobi)، دیریکله (Dirichlet) و آیزنشتاین (Eisenstein) تحصیل کند که یک فرصت مهم برای ریمان به شمار میرفت. اگر چه او بیشتر از آیزنشتاین یاد گرفت و استفاده از متغییرهای مختلط در تابع بیضوی را مورد بحث قرار داد اما دیریکله تأثیرگذارترین شخص بر او در این زمان بود. کلین (Klein) در این باره می‌گوید :

« ریمان با یک همفکری درونی قوی به دیریکله وابسته بود. دیریکله دوست داشت که همه چیز را با یک زمینه شهودی برای خود مشخص سازد. در کنار این تحلیل های منطقی و دقیق سؤالات اساسی ارائه می داد و تا حد ممکن از محاسبات طولانی خودداری می‌کرد. ریمان با این رفتارش موافق بود و آن را پذیرفته بود و مطابق با روش های دیریکله فعالیت می‌کرد »

کار ریمان همواره بر اساس استنباط شهودی بود که احساس می‌شد دقت لازم برای نتیجه گیری بی‌چون و چرا را ندارد. با وجود این نظریات عالی در کارهایش بسیار واضح‌تراست چون کارهایش خیلی با محاسبات طولانی پر نشده است. زمانی که در دانشگاه برلین بود تئوری کلی متغیرهای مختلط را بررسی کرد که اساس بعضی از کارهای بسیار مهمش را تشکیل می داد.

ریمان در سال 1849 به گوتینگن برگشت و پایان‌نامه Ph.D او (دکتری) که گائوس را متعجب ساخت در سال 1851 ارائه شد. با این وجود گاوس تنها شخص تاثیر گذار بر ریمان نبود. وبر (Weber) در مدتی که ریمان در برلین بود، از لیپزیگ (Leipzig) به استادی فیزیک در گوتینگن برگشته بود و ریمان به مدت 18 ماه همکارش بود. همچنین لیسینگ (Listing) در سال 1849 به عنوان استاد فیزیک در گوتینگن برگزیده شده بود. ریمان از وبر و لیسینگ پیش زمینه قوی از فیزیک نظری و از لیسینگ ایده‌های مهمی در مورد توپولوژی به دست آورد که در تحقیقات جدیدش موثر بود.

تولد هندسه نااقلیدسی

در دهم ژوئین 1854 هندسه جدیدی تولد یافت. موقعی که جرج برنارد ریمان سخنرانی معروف خود در دانشگاه گوتینگن آلمان را ارائه کرد، تئوری ابعاد بالاتر معرفی شد. ریمان در اقدامی چشم گیر و ناگهانی مانند گشودن درب اتاقی تاریک و نمناک به روی آفتاب گرم و درخشان تابستان خصوصیات حیرت انگیز فضای فرا ابعادی را به دنیا معرفی کرد. مقاله فوق‌العاده مهم و استثنایی او با نام «در باب فرضیاتی از اصول هندسه» ستونهای هندسه کلاسیک یونان را که در طول ۲۰۰۰ سال تمام انتقادهای افراد شکاک را با موفقیت دفع کرده بود در هم فرو ریخت. با فرو ریختن هندسه قدیمی اقلیدس که در آن تمام اشکال هندسی دو یا سه بعدی هستند، هندسه ریمان از خرابه‌های آن سر بر افرشت و قرار بود انقلاب ریمان کاربردهای وسیعی در آینده هنر و علوم داشته باشد و ظرف سه دهه از زمان سخنرانی وی تحت عنوان « بعد اسرار آمیز چهارم» تکامل هنر فلسفه و ادبیات اروپا را متاثر سازد.

در طول شش دهه بعد انیشتین با استفاده از هندسه چهار بعدی ریمان آفرینش و تکامل جهان را توضیح می‌دهد. صد و سی سال پس از آن سخنرانی فیزیکدان‌ها در تلاشند تا با استفاده از هندسه ده بعدی اتحاد قوانین جهان فیزیکی را تحقق بخشند. هسته کار ریمان تشخیص این نکته بود که در فضای فرا ابعادی قوانین فیزیکی سادهتر می‌شوند.

مسئله‌ای که توجه ریمان را به خود جلب کرده بود فروپاشی هندسه اقلیدسی یکی دیگر از ستونهای استوار ریاضیات بود که بیانگر سه بعدی بودن فضاست. علاوه بر این فضای سه بعدی یاد شده «تخت» می‌باشد (در فضای تخت کوتاه‌ترین فاصله بین دو نقطه یک خط راست است و این موضوع امکان انحنادار بودن فضا مانند سطح یک کره را منتفی می‌کند). در واقع کتاب اصول اقلیدس احتمالا بعد از انجیل تاثیر گذارترین کتاب تاریخ بود. پویا ترین مغزهای تمدن غرب برای دو هزار سال در برابر زیبایی و سحر کلام هندسه این کتاب در تحیر بوده اند. بر پایه این اصول هزاران کلیسای عالی بنا نهاده شدند. در نگاهی به گذشته این هندسه شاید بیش از حد موفق بود و در طول قرون جایگاهی همچون یک مذهب پیدا کرده بود. هر کسی که جرات به خرج داده و فضای انحنادار یا ابعاد بالاتر را مطرح می‌کرد مورد تکفیر قرار می‌گرفت. برای نسلهای متمادی دانش‌آموزان با اصول هندسه اقلیدسی کلنجار رفته‌اند : اینکه محیط یک دایره برابر حاصل ضرب قطر آن در عدد پی است و مجموع زوایای داخلی یک مثلث 180 درجه است.

ولی ریاضیدانان بزرگ در طول قرنها علیرغم تلاش‌هایشان موفق به اثبات این قضایای ساده و اغواکننده نشدند. در واقع ریاضیدانان اروپا بتدریج دریافتند که حتی کتاب اصول اقلیدس که 2300 سال مورد تکریم بود کتاب ناقصی است. با محدود کردن خود به سطوح تخت میتوان از هندسه اقلیدسی دفاع کرد اما اگر وارد دنیای سطوح انحنا دار شویم این هندسه عملا غلط از آب در می‌آید. از نظر ریمان هندسه اقلیدسی بخصوص در مقایسه با دنیا و تنوع غنی آن فاقد خلاقیت و نوزایی بود. شکلهای هندسی مسطح و ایده‌آل اقلیدسی را در هیچ جای طبیعت نمی توان مشاهده کرد. رشته کوه‌ها، امواج اقیانوس‌ها،ابرها، گردابها، شکلهای دایره‌های مثلثی و مربعی کامل نیستند. بلکه اشیاء منحنی هستند که به روشهای بی‌شماری خمیده و پیچیده شده‌اند. زمان انقلاب فرا رسیده بود اما چه کسی هدایت آن را در دست می‌گرفت و چه چیزی میتوانست جایگزین هندسه قدیمی گردد.

ریمان در برابر هندسه یونانی با دقت ریاضی ظاهری، قد علم کرد، هندسه‌ای که بنا به دریافت ریمان اصول آن در نهایت بر اساس بنیان‌های لرزان فهم عامه و باورهای فطری استوار بود، نه یک زمینه مستحکم منطقی، به گفته اقلیدس ، بدیهی است که نقطه هیچ بعدی ندارد و خط دارای یک بعد است : طول، صفحه دو بعد دارد : طول و عرض، یک جسم جامد سه بعد دارد : طول و عرض و ارتفاع. و این هندسه در همین جا متوقف می‌شود. هیچ چیز دارای چهار بعد نیست. این دریافت‌ها توسط ارسطوی فیلسوف نیز بازتاب داده می‌شد که ظاهرا اولین کسی بود که قاطعانه بیان کرد بعد چهارم فضایی، ناممکن می‌باشد. وی در کتابش به نام «در مورد آسمان» نوشت :

خط در یک بعد دارای اندازه است، صفحه در دو بعد و جسم جامد در سه بعد و فراتر از اینها هیچ بعدی وجود ندارد. چرا که فقط سه بعد وجود دارند.

برای هزاران سال ریاضیدان‌ها دائما مرتکب این اشتباه ساده ولی اساسی می‌شدند که بعد چهارم نمی‌تواند وجود داشته باشد، برای این که نمی‌توانیم تصویری از آن را در ذهن خود داشته باشیم.
شکاف عمیق، موقعی در هندسه اقلیدسی حاصل آمد که گاوس از شاگردش ریمان، در خواست کرد تا یک سخنرانی در مورد "بنیاد هندسه" ارائه دهد. گاوس خیلی علاقه‌مند بود تا ببیند آیا شاگردش می‌تواند در توسعه یک مدل جایگزین برای هندسه اقلیدسی موفق باشد یا نه ؟  (چند دهه قبل از آن، گاوس بطور شخصی، مطالعات عمیق و وسیعی در باب هندسه اقلیدسی انجام داده بود. وی حتی با همکارانش در مورد "کرم کتاب" هایی فرضی که می‌توانند در یک سطح کاملا دو بعدی زندگی کنند، صحبت کرده بود. وی در مورد این ایده به هندسه فضای فرا ابعادی نیز صحبت کرده بود. بهر حال، از آنجائی‌که گاوس شخصیت محافظه کارانه‌ای داشت، هیچ یک از کارهای خود را در مورد ابعاد بالاتر انتشار نداد زیرا احتمال ایجاد سرو صدا و اعتراض از طرف افراد کج اندیش و محافظه‌کار و متعصب می‌رفت. وی به تمسخر، چنین افرادی را «بیوتین» می‌نامید که یک قبیله عقب مانده ذهنی یونانی بودند.

با این همه، ریمان در هراس بود. با داشتن شخصیتی ترسو و حتی بیم صحبت کردن در مقابل مردم، قرار بود به درخواست استادش، برای تمام دانشکده، در مورد مشکل‌ترین مسئله ریاضیات قرن، سخنانی ایراد کند.
در طول ماه‌ها بعد، ریمان با رنج و مشقت شروع به تعمیم تئوری فرا ابعادی نمود و در این راه تا به خطر افتادن سلامتی خود و ناراحتی اعصاب پیش رفت. بخاطر وضعیت مالی رقت انگیزش، بنیه جسمی وی نیز در معرض خطر قرار گرفت. او مجبور بود که به شغلهای کم درآمدی مانند معلمی سر خانه بپردازد تا کمکی نیز به خانواده‌اش بکند. گذشته از اینها، بخاطر تلاش در توضیح مسائل فیزیک، از مسیر کاری خودش منحرف می‌شد. بخصوص اینکه وی به یک پروفسور دیگر بنام "ویلهلم وبر" در انجام آزمایشاتی در زمینه تحقیقاتی تازه و جذاب الکتریسیته کمک می‌کرد.

ریمان تمام وقت خود را وقف آزمایشگاه وبر ساخته بود. بخاطر قبول مسئولیت آماده کردن یک سخنرانی دقیق و موشکافانه در مورد "بنیاد هندسه" برای تامین خانواده خود و نیز انجام دادن آزمایشات علمی، در نهایت سلامتی ریمان به خطر افتاد و در سال 1854 دچار اختلال عصبی گردید.

سرانجام ریمان، علی‌رغم بیماری‌های مکرر خود، تصویر تازه و تکان دهنده‌ای از مفهوم "نیرو" ارائه نمود. از زمان نیوتن، دانشمندان نیرو را به عنوان عامل اندرکنش لحظه‌ای بین دو جسم دور از هم در نظر می‌گرفتند. این موضوع را فیزیکدان‌ها، کنش از فاصله نام‌گذاری کردند، بدین معنی که یک جسم می‌تواند حرکت اجسام دورتر را به طور آنی تحت تاثیر قرار دهد. مکانیک نیوتنی، بدون شک می‌توانست حرکت سیاره‌ها را توصیف کند ولی در طول قرون، منتقدین در مورد غیر طبیعی بودن موضوع کنش از فاصله بحث می‌کردند، اینکه یک جسم بتواند جهت حرکت جسم دیگر را بدون اینکه حتی تماسی با آن داشته باشد، تغییر دهد.

ریمان، تصویر فیزیکی جدید و کاملا متفاوتی را ارائه نمود. مانند (کرم های کتاب) گاوس، وی گونه‌ای از موجودات دو بعدی را که بر روی یک صفحه کاغذ زندگی می‌کردند، در نظر گرفت. ولی راه‌حل مهم ریمان این بود که موجودات را بر روی یک صفحه کاغذ "مچاله شده" در نظر گرفت. این موجودات چه تصوری از دنیای اطراف خود داشتند؟ دریافت ریمان این بود که از نظر آنها، دنیایشان کاملا تخت می‌نماید. بخاطر اینکه بدنهای آنها با صفحه کاغذ مچاله شده بودند، هرگز متوجه انحنای دنیای خود نمی‌شدند. با این وجود، ریمان عقیده داشت که اگر این موجودات سعی در حرکت روی این صفحه کاغذ مچاله شده بکنند،"نیروی نامرئی" و اسرار آمیزی را احساس می‌کنند که مانع از حرکت آنها در یک خط مستقیم می‌شود. هر دفعه که این موجودات از روی چین و چروکهای صفحه حرکت می‌کردند، بدنهایشان به چپ و راست فشار داده می‌شد. بدین ترتیب، با رد کردن اصل کنش از فاصله، ریمان بعد از 200 سال، اولین تکان اساسی را به فیزیک نیوتنی وارد نمود. از نظر ریمان، "نیرو نتیجه‌ای از هندسه است" در ادامه، ریمان بجای صفحه کاغذ دو بعدی، جهان سه بعدی ما را در بعد چهارم پیچیده شده، جایگزین کرد. در هم پیچیدگی جهان برای ما روشن و واضح نیست. با اینهمه، اگر ما سعی می‌کردیم تا در یک خط راست حرکت کنیم، بلافاصله متوجه می‌شدیم که این کار ما یک ایرادی دارد. ما مانند آدمهای مست، تلو تلو می‌خوردیم گویی که نیرویی نامریی ما را به چپ و راست هل می‌دهد. ریمان به این نتیجه رسید که الکتریسیته، مغناطیس و گرانش ناشی از درهم مچاله شدن جهان سه بعدی ما در بعد نامرئی چهارم می‌باشد. بنابراین "نیرو" موجودیت مستقلی ندارد بلکه فقط اثری ظاهری است که بخاطر تغییر شکل هندسی ایجاد می‌شود.

ریمان با معرفی بعد چهارم مکانی، بطور اتفاقی با یکی از موضوعات اصلی فیزیک نظری مدرن مواجه شد، اینکه وقتی طبیعت در فضای با ابعاد بالاتر بیان شوند، ساده تر بنظر می‌رسند. وی سپس سعی در ایجاد یک زبان ریاضی داشت که بوسیله آن، بتواند این عقیده را توضیح دهد. چند ماه طول کشید تا ریمان توانست از ناراحتی عصبی خود، خلاصی یابد. در نهایت، وقتی که سخنرانی خود را در سال 1854 ارائه نمود، مورد استقبال گسترده ای قرار گرفت. با نگاهی به گذشته، معلوم می‌شود که سخنرانی وی، بدون شک یکی از مهمترین سخنرانی‌های عمومی در تاریخ ریاضیات بود. به زودی در سراسر اروپا شایع گشت که ریمان مشخصا پا را فراتر از هندسه اقلیدسی نهاده است، هندسه‌ای که در طول دو هزار سال گذشته، حاکم بود. خبرهای مربوط به سخنرانی در تمام مراکز آموزشی اروپا پخش شد و در مجامع آکادمیک، از سهم عمده ریمان در پیشبرد ریاضیات ستایش و قدردانی به عمل آمد. مطالب وی به چندین زبان ترجمه شد و تکانی در ریاضیات ایجاد کرد. استناد به هندسه اقلیدس اهمیت قبلی خود را از دست داده بود.
مانند بیشتر کارهای برجسته در فیزیک و ریاضیات، درک هسته اصلی مقاله مهم ریمان، کار مشکلی نیست. ریمان، کار خود را با قضیه معروف فیثاغورث، یکی از کشف‌های مهم یونانی ها در ریاضیات، شروع کرد. این قضیه رابطه‌ای بین طول سه ضلع یک مثلث قائم‌الزاویه ایجاد کرده و بیان می‌دارد که مجموع مربعات اضلاع کوچکتر برابر با مربع ضلع بزرگتر، یعنی وتر می‌باشد. به عبارتی دیگر، اگر b , a طول دو ضلع کوتاهتر و c طول وتر باشد،

البته قضیه فیثاغورث، اساس تمام کارهای معماری است. هر بنایی که در این سیاره ساخته می‌شود، بر روی این قضیه استوار است.

در این صورت  این قضیه، برای فضای سه بعدی هم به راحتی قابل تعمیم است. به این بیان که مجموع مربعات سه ضلع مجاور به هم در یک مکعب برابر با مربع قطر مکعب است. لذا اگر a، b و c نشانگر یالهای مکعب و d معرف طول قطر مکعب باشد، در این صورت:

 a²+b²+c²=d²

حال به سادگی می‌توان این قضیه را به فضای N بعدی تعمیم داد. فرض کنید در یک مکعب N بعدی، a، b، c و... طول یال‌های این "ابر مکعب" بوده و z طول قطر آن باشد. در این صورت :

a²+b²+c²+....=z²

موضوع قابل توجه این است که با وجود ناتوانی ذهن ما برای تصور این مکعب N بعدی، نوشتن فرمولی برای اضلاع آن، ساده می‌باشد. (این یک خصوصیت متداول در کار با ابر فضا است. از نظر ریاضی، سر و کار داشتن با فضای N بعدی مشکل‌تر از سر و کار داشتن با فضای سه بعدی نیست. تعجب آور نیست که بتوان بر روی یک صفحه کاغذ، خواص جسمی با ابعاد بالاتر را که توسط ذهن‌های ما قابل تصور نیستن، به طور ریاضی توصیف کرد). در ادامه کار، ریمان این معادلات را برای فضای های با ابعاد اختیاری تعمیم داد. این فضا‌ها یا تخت هستند یا انحنا دار. اگر فضا تخت باشد، در این صورت اصول موضوعی رایج اقلیدس کاربرد دارد : کوتاهترین فاصله بین دو نقطه یک خط مستقیم است، یک صفحه دارای انحنای صفر میباشد. در هندسه اقلیدسی زوایای داخلی یک مثلث برابر 180 درجه می‌باشد و خطوط موازی هرگز همدیگر را قطع نمیکنند.

در هندسه نااقلیدسی ، یک کره دارای انحنای مثبت میباشد، مجموع زوایای داخلی مثلث بیشتر از 180 درجه بوده و خطوط موازی همیشه یکدیگر را قطع میکنند (خطوط موازی شامل کمان‌هایی هستند که مرکز آنها با مرکز کره یکی است )، یک سطح به شکل زین دارای انحنای منفی است،مجموع زوایای داخلی کمتر از 180 درجه است، بی‌نهایت خطوط موازی با یک خط مفروض وجود دارند که از یک نقطه ثابت عبور میکنند.
هدف ریمان معرفی روشی تازه در ریاضیات بود که وی را قادر به توصیف تمام سطوح، صرف‌نظر از میزان انحنای آنها بکند. این امر ریمان را بطور غیر قابل اجتنابی به مطرح کردن دو باره مفهوم میدان فاراده سوق داد. همان‌طور که گفته شد، میدان فاراده یک ناحیه از فضای سه بعدی را اشغال می‌کرند که می توان به هر نقطه‌ای از آن فضا، مجموعه ای از اعداد را که توصیف کننده نیروی مغناطیسی یا الکتریکی آن موقعیت می‌باشند، نسبت دهیم. ایده ریمان، معرفی مجموعه‌ای از اعداد در هر نقطه‌ای از فضای بود که بتوانند مقدار انحنا یا تاب آن فضا را توصیف کنند.

برای مثال، در یک صفحه دو بعدی معمولی، ریمان یک مجموعه سه عددی را برای هر نقطه نسبت داد که توصیف کننده کامل مقدار خم در آن نقطه بود. وی متوجه شد که در فضای چهار بعدی فضایی، برای هر نقطه، نیاز به مجموعه‌ای ده عددی برای توصیف خواص آن می‌باشد. صرف‌نظر از میزان مچاله شدگی یا پیچش فضا، این مجموعه ده عددی در هر نقطه، برای مشخص کردن اطلاعات لازم درباره آن فضا کافی است. اجازه دهید این ده عدد را با علائم g₁₁,g₁₂,g₁₃,... نشان دهیم ( در تحلیل یک فضای چهار بعدی، اندیس پایین می‌تواند از یک تا چهار تغییر کند). در اینصورت مجموعه ده عددی ریمان را می توان با یک آرایش متقارن، آرایش داد.

g₁₁   g₁₂   g₁₃   g₁₄
g₂₁   g₂₂   g₂₃   g₂₄
g₃₁   g₃₂   g₃₃   g₃₄ g₄₁   g₄₂   g₄₃   g₄₄

(بنظر می رسد که اینجا با 16 مولفه سر و کار داریم، ولی g₁₂=g₂₁ و g₁₃=g₃₁ و غیره. بنابراین در واقع فقط ده مولفه مستقل از هم وجود دارند). امروزه، به این مجموعه اعداد «تانسور متریک» ریمان گفته می‌شود. در حالت کلی هر چه اندازه تانسور متریک بزرگتر باشد، مچاله شدگی صفحه نیز بیشتر خواهد بود. تانسور متریک به ما ابزاری جهت اندازه‌گیری مقدار انحنای صفحه در نقطه، بدون توجه به میزان مچاله شدگی آن ارائه می‌دهد. اگر این صفحه مچاله شده را کاملا صاف کنیم،دراین صورت به فرمول فیثاغورث می رسیم. ریمان توسط تانسور متریک خود، توانست یک ابزار قوی برای توصیف فضاهایی با ابعاد دلخواه، و با هر انحنایی را بنا نهد.

ریمان با تعجب دریافت که تمام این فضاها، خوش تعریف و خود سازگار هستند. قبلا گمان میرفت که در صورت تحقیق در مورد دنیای ممنوعه ابعاد بالاتر، تضادهای بسیار زیادی بروز خواهند نمود، با این وجود ریمان بر خلاف انتظارش هیچ‌گونه تضادی مشاهده ننمود. در حقیقت تعمیم موضوع به فضای N بعدی برای ریمان، موضوع ساده‌ای می‌نمود. در این حالت، تانسور متریک مشابه خانه‌های یک صفحه شطرنجی N*N خواهند بود. وقتی که ما اتحاد تمام نیروها را مورد بحث قرار دهیم، این موضوع کاربردهای فیزیکی خیلی زیادی پیدا خواهد نمود.
(خواهیم دید که رمز اتحاد، بسط دادن تانسور متریک ریمان به فضای N بعدی و سپس تجزیه کردن آن به اجزای مستطیلی است. هر قسمت مستطیلی، متناظر با یک نیروی متفاوت است. با این ترتیب می‌توانیم نیروهای مختلف طبیعت را با مرتب کردن آنها در تانسور متریک، مانند قطعات یک پازل، توصیف کنیم. این موضوع بیان ریاضی اصلی است که نشان می‌دهد فضای فرا ابعادی، قوانین طبیعت را یکی میکند، این که "فضای کافی" برای اتحاد آنها در فضای N بعدی موجود است. به عبارت دقیق‌تر، در متریک ریمان،"فضای کافی" برای اتحاد نیروهای طبیعت وجود دارد.)

ریمان پیشرفت دیگری در فیزیک را پیش‌بینی کرد. وی یکی از اولین افرادی بود که "فضا های هم بند چندگانه" – کرم چاله‌ها – را مورد بررسی قرار داد. برای تصور این مفهوم، دو صفحه کاغذ برداشته و یکی از آنها را روی صفحه دیگر بگذارید. حال با قیچی برشی کوچک بر روی هر یک از صفحات ایجاد کنید. سپس درامتداد این دو برش، صفحات را به هم بچسبانید (از نظر توپولوژی – مکان شناسی : علم بررسی خواصی از فضا ها که با کشیدن یا فشردن تغییرنمیکند -- طول کرم‌چاله، صفر در نظر گرفته شده است).
اگر یک حشره که در صفحه بالایی زندگی می‌کند، روزی بر حسب اتفاق به داخل شکاف برود، خودش را در صفحه پایین خواهد یافت. در این صورت، این حشره سر در گم خواهد شد زیرا هیچ چیز در جای صحیح خود قرار ندارد. بعد از مدتی سعی و تلاش، متوجه خواهد شد که می‌تواند با ورود دوباره به برش ایجاد شده بار دیگر در دنیای معمول خود ظاهر شود. این حشره، تا زمانی که دور از شکاف حرکت کند، دنیایش عادی به نظر میرسد، ولی اگر سعی در حرکت میانبر از طریق شکاف بکند، با مشکل مواجه خواهد شد. برش‌های ریمان، یک مثال از کرم‌چاله می‌باشند که دو فضا را به هم وصل می‌کند (با این تفاوت که د ر این حالت طول کرم‌چاله صفر می‌باشد.) برش های ریمان به طور موثرتری توسط ریاضیدانی به نام لویس کارل در کتابش تحت عنوان "از میان آینه" مورد استفاده واقع شد. برش ریمان، که انگلستان را با یک سرزمین عجایب ارتباط می‌دهد یک آینه است.

امروزه برش‌های ریمان به دو صورت باقی مانده‌اند، در شکل اول این که، در طول هر دوره کارشناسی ارشد ریاضی در دنیا، زمانی مطرح می‌شوند که کاربرد آنها در تئوری "الکترو استاتیک یا نگاشت همدیس" بحث می‌شود. و در شکل دوم برش‌های ریمان را در بخش‌هایی از فیلم " ناحیه گرگ و میش " می‌توان پیدا کرد. ( باید تاکید نمود که خود ریمان، این برش‌ها را به عنوان ابزاری جهت امکان مسافرت بین جهان‌ها، تصور نمی‌کرد).

حضور ریمان در فیزیک به خاطر کارهایش همچنان ادامه داشت. حتی وی در سال 1858 اعلام کرد که سرانجام موفق شده است به بیان واحدی از نور و الکتریسیته دست پیدا کند. وی نوشت که "من کاملا متقاعد شده ام که تئوری‌ام تئوری درستی است، و در عرض چند سال آینده، این موضوع روشن خواهد شد." با اینکه تانسور متریک، روش موثری برای توصیف هر فضای انحنا یافته در هر بعدی را در اختیار ریمان قرار می داد، ولی وی معادلات دقیقی را که تانسور متریک از آنها تبعیت بکند نمی‌دانست، یعنی از این موضوع که چه چیزی باعث مچاله شدن کاغذ می‌شود اطلاع نداشت. متاسفانه تلاشهای ریمان برای حل مسئله، بخاطر فقر وحشتناکی که گرفتارش بود، به نتیجه ای روشن نمی‌رسید. موفقیت‌های ریمان برایش پولی به ارمغان نمی‌آورد.

در سال 1858 وی دچار اختلال عصبی دیگری شد. بعد از سالیان طولانی، وی به مقام گائوس در گوتینگن منصوب شد که افراد زیادی در حسرت آن بودند. ولی دیگر خیلی دیر شده بود. یک عمر زندگی فقیرانه، وی را در هم شکسته بود.

بطور خلاصه، ریمان پا را فراتر از بنیان نهادن ریاضیات ابر فضا، گذاشت. در نگاهی به گذشته، متوجه می‌شویم که ریمان برخی از موضوعات اصلی در فیزیک مدرن را نیز پیش‌بینی نموده بود. خصوصا موارد زیر را :

•  وی فضای فرا ابعادی را برای ساده سازی قوانین طبیعت بکار برد. بنظر وی الکتریسیته و مغناطیس و نیز گرانش تنها تاثیراتی از مچاله شدن و در هم پیچیدگی فضای فرا ابعادی می‌باشند.
• وی مفهوم کرم‌چاله‌ها را پیش‌بینی نمود. برش‌های ریمان، ساده‌ترین مثالها از فضاهای همبند چند گانه هستند.
•  ریمان، گرانش را به عنوان یک میدان بیان نمود. تانسور متریک، به دلیل آنکه نیروی گرانشی را ( بواسطه انحنا ) در هر نقطه‌ای از فضا توصیف می‌کرند. موقعی که به گرانش اعمال می شود، دقیقا مفهوم میدان فاراده را دارا می‌باشد.

ریمان نمی‌توانست کار خود بر روی میدان‌های نیرو را کامل کند، زیرا وی به معادلاتی که الکتریسته، مغناطیس و گرانش از آنها تبعیت می‌کرند، دسترسی نداشت. بعبارت دیگر نمی‌دانست که جهان دقیقا چگونه مچاله شده و نیروی گرانش را تولید می‌کرند. وی کوشید تا معادلات مربوط به میدان الکتریسیته و مغناطیس را کشف کند. ولی قبل از اینکه موفق به اتمام پروژه‌اش شود، دار فانی را وداع گفت. تا زمان مرگش، وی هنوز هیچ راهی برای محاسبه اینکه چه مقدار مچاله شدگی برای توصیف نیروها لازم است، پیدا نکرده بود. پیشرفت‌های عظیم در این زمینه، به ماکسول و اینشتین واگذار شده بود.

سرانجام طلسم شکسته بود. ریمان در طول زندگی کوتاه خود، طلسمی را که بیش از دو هزار سال قبل توسط اقلیدس ایجاد شده بود، شکست. تانسور متریک ریمان سلاحی بود که ریاضیدان‌های جوان با آن در مقابل بوتیانها که در برابر هر نوع اظهار عقیده در مورد ابعاد بالاتر به مخالفت بر می‌خواستند، ایستاد. کسانی که از آراء ریمان تبعیت می‌کردند، متوجه شدند که راه خوبی برای صحبت از دنیاهای نامرئی پیدا کرده‌اند. بزودی نتایج تحقیقات در سراسر اروپا به بار نشست. دانشمندان برجسته، شروع به عامه فهم کردن این ایده برای مردم عادی نمودند. هرمان فون هلمهولتز که شاید معروفترین فیزیکدان آلمانی نسل خویش بود و عمیقا تحت تاثیر کارهای ریمان قرار گرفته بود، درباره ریاضیات حاکم بر دنیای موجودات هوشمندی که بر روی یک کره یا توپ زندگی می‌کردند، سخنان زیادی برای عموم مردم ایراد نمود و یا به رشته تحریر در آورد.

بر طبق نظر هلمهولتز، این موجودات با قدرت استدلالی مشابه ما انسانها، بطور مستقل کشف می‌کردند که تمام فرضیات و قضایای اقلیدس بی فایده‌اند. برای مثال، بر روی کره، مجموع زوایای داخلی یک مثلث، 180 درجه نمی شود. "کرم کتاب" که گاوس قبلا برای اولین بار در مورد آنها سخن گفته بود، حال خود را ساکنین کره های دو بعدی هلمهولتز می یافتند.

هلمهولتز نوشت :

" اصول موضوعی هندسه باید متناسب با نوع فضایی تغییر کنند که در آن موجوداتی با قدرت استدلال شبیه ما انسانها، زندگی می‌کرنند. وی در کتاب خود تحت عنوان سخنرانیهای مشهور در باره موضوعات علمی (1881) به خوانندگانش گوشزد نمود که تصور بعد چهارم برای ما امکانپذیر نیست. در واقع، او بیان داشت که " چنین " تصویری " برای ما، همانقدر غیر ممکن است که تصور رنگها برای کسی که نابینا بدنیا آمده است ".

برخی از دانشمندان که مبهوت زیبایی کار ریمان شده بودند، تلاش کردند تا برای چنین ابزار قوی، کاربردهای فیزیکی پیدا کنند. در حالی‌که بعضی از دانشمندان کاربردهای بعد بالاتر را کشف میکردند، بقیه دانشمندان به مسایل عملی و ملموستری مانند نحوه غذا خوردن یک موجود دو بعدی می‌پرداختند. برای اینکه موجودات دو بعدی گاوس بتوانند غذا بخورند، دهانشان باید معطوف به یک جهت باشد. حال اگر لوله گوارشی این موجودات را رسم کنیم، متوجه می شویم که این مسیر، بدن آنها را کاملا به دو قسمت تقسیم می‌کرند. بنابر این در صورتیکه غذا بخورند، بدنشان به دو تکه مجزا تقسیم می شود. در واقع، هر لوله‌ای که دو روزنه بدنشان را به هم متصل می‌سازد،آنها را به دو تکه مجزا تقسیم میکند. این امر، ما را با یک انتخاب دشوار مواجه می سازد. یا اینکه این مردم مانند ما انسان‌ها غذا می خورند و لذا بدنشان از هم جدا می‌شود و یا اینکه از قوانین زیست شناسی متفاوتی تبعیت می‌کنند.

متاسفانه ریاضیات پیشرفته ریمان از سطح درک فیزیک قرن نوزدهم، خیلی جلو افتاده بود. هیچ اصل فیزیکی برای جهت دادن به تحقیقات بیشتر وجود نداشت. مجبور بودیم تا یک قرن صبر کنیم تا فیزیکدان‌ها هم سطح ریاضیدان‌ها بشوند. اما این موضوع مانع از آن نشد که دانشمندان قرن نوزدهم به حدسیات بی‌پایان در مورد شکل موجودات چهار بعدی نپردازند. بزودی، آنها دریافتند که چنین موجودات چهار بعدی تقریبا نیروهای خداگونه خوهند داشت.

در نگاهی به گذشته در می‌یابیم که سخنرانی مشهور ریمان بوسیله متصوفین، فیلسوفان و هنرمندان در بین عموم مردم پخش شد، هر چند به درک بیشتر ما از طبیعت کمک زیادی نمی‌کرد. از دیدگاه فیزیک نوین، همچنین می‌توانیم ببینیم که چرا بین سالهای 1860 تا 1905 در درکمان از ابر فضا گشایشی بوجود نیامده است.

اولا تلاشی صورت نگرفت تا با استفاده از ابعاد بالاتر، قوانین طبیعت ساده‌تر شوند. بدون اصل راهگشا و بنیادین ریمان – که قوانین طبیعت در ابعاد بالاتر ساده می‌شوند – دانشمندان در این مدت، تنها در تاریکی به لمس موضوع می‌پرداختند. اندیشه پر بار ریمان در مورد استفاده از هندسه – یعنی ابر فضای مچاله شده – برای توضیح اساس یک " نیرو " در آن سالها فراموش شده بود. ثانیا هیچ کوششی برای استفاده از مفاهیم میدان فاراده یا تانسور متریک ریمان برای پیدا کردن معادلات میدانی که ابر فضا از آن تبعیت می‌کرد به عمل نیامد. ابزار ریاضی که توسط ریمان توسعه داده شد، بر خلاف مقاصد اصلی وی موضوع ریاضیات محض قرار گرفت. بدون تئوری میدان، نمی توان در مورد ابر فضا ابراز نظر کرد. بنابراین با شروع قرن جدید بدگمانان (با توجیهاتی) ادعا کردند جز تحریک مردم با داستانهای ارواح، هیچ انگیزه فیزیکی برای معرفی بعد چهارم وجود ندارد. با این وجود، این وضعیت نا مطلوب به زودی تغییر می یافت. ظرف چند دهه تئوری بعد چهارم (زمان) برای همیشه مسیر تاریخ را تغییر می‌داد. این تئوری، بمب اتمی و تئوری خود آفرینش را در اختیارمان می گذاشت و فردی که قرار بود این کار را انجام دهد فیزیکدان گمنامی بنام آلبرت اینشتین بود.

پاورقی: هندسه ریمانی

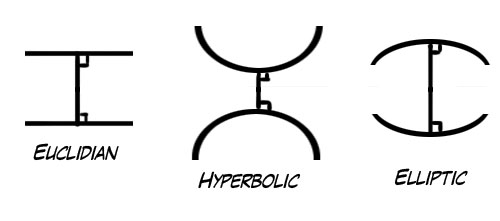
هندسه ریمانی با هندسه بلیایی و لباچفسکی فرق بارز دارد، مثلا آنان به رسم بیشتر از یک خط به موازات خط معین از نقطه معین قائل بودند، اما ریمان موازی را انکاررد. با این که آنها مجموع زاویه‌های مثلث را کوچکتر از دو قائمه گرفتند و ریمان بزرگتر از آن.
هندسه نااقلیدسی لیایی و لباچفسکی را هندسه هذلولوی (یپربولیک) و هندسه ریمان را هندسه بیضوی  (الیپتیک) نامیده‌اند.

 

مرگ ریمان

وی با وجود ابتلا به بیماری سل و تحمل سال‌ها رنج و کسالت، لحظه‌ای از تلاش و علم‌آموزی غافل نبود. مانند بسیاری از بزرگترین ریاضیدانان در طول تاریخ، وی نیز قبل از اینکه موفق به تکمیل تئوری هندسی گرانشی و الکتریستیه و مغناطیس شود، از دنیا رفت. ریمان در سن ۳۹ سالگی و در اوج بلوغ فکری درگذشت.

گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir