اراتوستن یا اراتستن یا اراتوستنِس (به یونانی: Ἐρατοσθένης) ( تا ۱۹۴ پیش از میلاد) ریاضیدان، شاعر، ورزشکار، جغرافیدان و ستارهشناس یونانی دوران اسکندر بود. اراتوستن اولین کسی بود که توانست محیط کره زمین را با استفاده از تفاوت زاویه تابش خورشید در اسکندریه و آتن بدست آورد.
زندگی
اراتوستن در سال 276 قبل از میلاد در شهرسیرن (شهری در لیبی کنونی) متولد شد. پس از تحصیل در آتن، پادشاه اسکندریه (بطلمیوس سوم) وی را برای تعلیم فرزندش از آتن به اسکندریه احضار کرد و در سال 240 قبل از میلاد به ریاست کتابخانه بزرگ اسکندریه منصوب شد که این افتخار مهمی بود.

او از بزرگترین فضلای اسکندریه بود، نه فقط ریاضیدانی برجسته بلکه جغرافی دانی قابل و مورخی دقیق نیز به شمار میآمد. آثار او در ریاضیات، جغرافیا، فلسفه، گاهشماری، نقد ادبی و دستور زبان و نیز شعر بسیار مشهور بودند.
وی از دوستان ارشمیدس بود و چند سالی پس از اقلیدس میزیست و جامع علوم زمان خود بود. معمولاً او را «بتا» دومین حرف الفبای یونانی مینامیدند. علت این وجه تسمیه این بود که وی دومین فرزانه در بین هم عصرانش بود. برخی معتقدند که منشأ این لقب، آن است که اطاق وی در دانشگاه اسکندریه اطاق شماره ی 2 بوده است.
یکی از آثار برجسته اراتوستن، کتاب Platonicus بوده است که در آن به بحث درباره مفاهیم مقدماتی هندسه و حساب پرداخته است و بحثی هم در زمینه موسیقی دارد. در نامهای که وی به بطلمیوس سوم نوشت، تاریخچه مسأله معروف تضعیف مکعب را خاطر نشان کرد و برای به دست آوردن راه حل مسالهای در هندسه به ترسیم دستگاهی مکانیکی و روش کار آن پرداخت. در حساب، روش غربال را برای یافتن اعداد اول ابداع نمود.
محاسبه شعاع کره زمین
او یک روز هنگام مطالعه دریافت که اطلاعات لازم برای محاسبهی محیط کره زمین را در اختیار دارد. او دریافته بود هنگام انقلابین (اصطلاح اخترشناسی) در ظهر، آفتاب در شهر آسوان مصر هیچ سایهای ندارد به گونهای که نور خورشید قادر است به طور مستقیم به ته یک چاه برسد، یعنی اینکه نور خورشید به صورت کاملا عمود به آسوان میتابد.
اراتوستن در چنین روزی درست هنگام ظهر که در آسوان سایه وجود ندارد در شهر اسکندریه سایه را اندازه گیری کرد، چاره ای نبود جز این که زمین را کروی درنظر بگیرد. چون سایه در اسکندریه نسبت به خط عمود هفت درجه بود، براساس اندازهگیری اراتوستن میان اسکندریه و آسوان 7 درجه فاصله بود. او با سفر میان دو شهر اسکندریه و آسوان فاصله آنها را 5000 استادیوم (واحد اندازه گیری در آن زمان «استادیوم» بود) اندازهگیری کرد. به این ترتیب هفت درجه از 360 درجه 5000 استادیوم اندازه گیری شده بود، پس محیط زمین براساس محاسبات اراتوستن 250000 استادیوم بود.
از آنجا که دانشمندان در مورد طول واقعی یک استادیوم یونانی اختلاف نظر دارند، غیر ممکن است بتوانیم دقت این اندازه گیری را تعیین کنیم. اما طبق بعضی از محاسبهها گفته می شود خطای این اندازه گیری حدود 5 درصد است.
اراتوستن در ضمینه جغرافیا نیز کارهای مهمی انجام داده است. او آثاری از خود بجای گذاشته که برای جغرافیای ایران قدیم هم گرانبهاست. استرابون در کتابهای خود نام او را بسیار آورده و گفتههای او را سند دانسته است. اراتوستن نخستین نویسنده خارجی است که نام ایران را یاد کرده است و قسمتی از ایران را آریانا نامیده است.

دلایل کم دقتی اراتستن
اختلاف در محاسبه اراتستن با اندازه واقعی به دلایلی چند از جمله موارد زیر می باشد :
- اندازهگیری فاصله بین دوشهر با دقت انجام نشده بود ( چون به وسیله کاروان شتر انجام گرفته بود )
- وسیله و ابزار دقیق اندازه گیری زاویه وجود نداشت.
- شهر اسکندریه و اسوان در روی یک نصف النهار نیستند.
- شکل واقعی زمین کروی نبوده ، بلکه یک شبه بیضی میباشد.
امروزه اندازهگیریهای دقیق نشان میدهد که قطر استوایی زمین 43 کیلومتر از قطر قطبی آن بیشتر است. در واقع ، قطر استوایی زمین 12756 کیلومتر و قطر قطبی آن 12713 کیلومتر است.
اندازهگیریهای دقیقتر
پس از اراتوستن، دانشمند دیگری به نام پوسید و نیومن (135_51 قبل از میلاد) میحط زمین را محاسبه کرد. بدین طریق که این دانشمند متوجه شد ستاره کانوپوس در هنگام غروب در افق شهر رودس مشاهده میگردد در صورتی که همین ستاره در اسکندریه در همان هنگام با افق زاویه 7.5 درجه میسازد. در نتیجه محیط کره زمین را 44400 کیلومتر محاسبه کرد که با مقدار واقعی آن 11 درصد اختلاف دارد. دلایل این اختلاف نیز مانند دلایل روشن اراتوستن میباشد.
ولی اولین اندازهگیری دقیق (تقریبا دقیق) شعاع زمین در سال 1535 میلادی توسط یک دانشمند و طبیب فرانسوی به نام «فرنل» انجام گرفت که محیط زمین 40044 کیلومتر حاصل شد که اختلاف آن با مقدار حقیقی یک در هزار بوده و سپس پیکارد با استفاده از روش مثلث بندی، پیرامون زمین را 40036 کیلومتر محاسبه کرد.
کارهای مهم دیگر اراتوستن
- پیدا کردن روش غربال کردن، راهی برای یافتن اعداد اوّل (شرح در پاورقی)
- احتمالاّ پیدا کردن فاصله ی زمین تا خورشید که امروزه واحد نجومی نامیده میشود.
- او نقشهای از ستارگان دارای 675 ستاره ترسیم کرد که هم اکنون در دست نیست.
- نقشهای از جهان شناخته شده برای یونانیان تا آن زمان؛ از جرایز بریتانیا تا سریلانکا و از دریای مازندران تا اتیوپی
- نقشهای از خطّ سیر نیل تا خارطوم
- تقویمی با سالهای پرشی؛ که اراتوستن در آن سعی کرد روزهای مختلف و اتّفاقات مختلف را در زمینه ادبیات و سیاست از زمان خود تا جنگ تروی حساب کند.
- حساب فاصله زمین تا ماه
- اندازهگیری شیب مدار زمین به دور خورشید با 7 درجه خطا
- کارهایی در زمینه ی تئاتر و اخلاق

غربال اراتستن
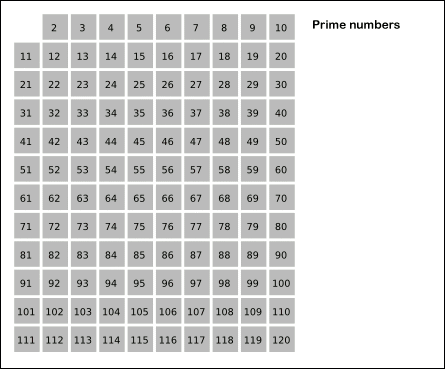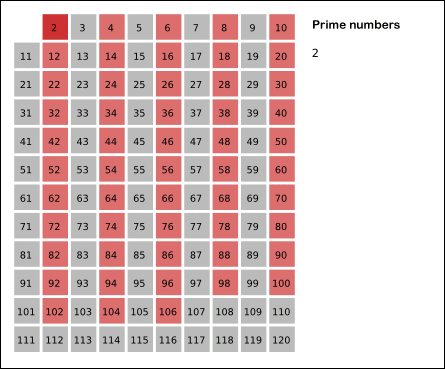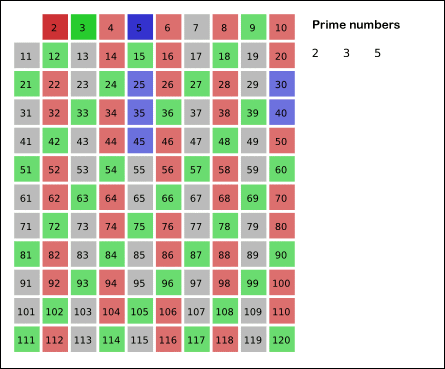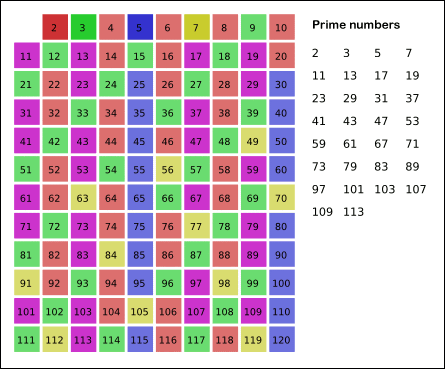
برای تشکیل فهرست همه عددهای اول تا یک عدد صحیح مفروض n میتوان همه عددهای صحیح کوچکتر از n را به ترتیب نوشت، نخست همه آنهایی را که مضرب 2 هستند خط زده سپس همه آنهایی را در میان اعداد باقیمانده که مضرب 3 هستند خط زده و همینطور به حذف سپس همه آنهایی را در میان اعداد باقیمانده که مضرب 3 هستند خط زد، و همینطور به حذف اعداد مرکب ادامه داد تا هیچ عدد مرکبی باقی نماند. این فرایند که به «غربال اراتستن» معروف است، تمام عددهای اول تا n را مشخص میسازد. جدولهای کاملی از عددهای اول تا حدود 10000000 به تدریج به وسیله صورتهای ظریفتری از این روش تهیه شدهاند، و این جدولها توده عظیمی از دادههای تجربی درباره توزیع و ویژگیهای اعداد اول در اختیار ما میگذارند. براساس آنها میتوانیم حدسهای بسیار موجهی بزنیم (چنانکه گویی نظریه اعداد یک علم تجربی است) که اثبات آنها اغلب بسیار دشوار است.
مرگ
اراتوستن در سنین کهولت، نابینا شد و چون میدانست که بیناییاش باز نخواهد گشت، آنقدر از خوردن غذا امتناع کرد تا سرانجام در سال 194 قبل از میلاد از گرسنگی جان سپرد.
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
![]()


