گام به گام ریاضی نهم - فصل ۳ - استدلال و اثبات در هندسه
.
.
.
فصل سوم (استدلال و اثبات در هنسه) کتاب ریاضی پایه نهم با تصاویری از دانههای برف آغاز میشود. بارش برف از آسمان، رحمت الهی را با خود به زمین میآورد و در عین حال نماد زیبایی زمستان است. اما شاید جالب باشد بدانید که این دانههای زیبای متقارن که اغلب شش شاخه هستند، علیرغم آنکه میلیاردها دانهاند، اما هر کدام شکل منحصر به خود را دارند و هیچ دو تایی از آنها «همنهشت» نیستند.
در این رابطه: چرا بلورهای برف شش پر و متقارن و سفید هستند؟!
مطالب این فصل پایه و اساس هندسه در دوره متوسطه دوم میباشد و کمک بسیار زیادی به یادگیری هندسه در سالهای بعد میکند. به همین دلیل دانشآموزان پایه نهم باید این فصل را به خوبی یاد بگیرند و مطالب آن را به خوبی درک کنند.
با حکمت و اندرز نیکو به راه پروردگارت دعوت نما و با آنها به نیکوترین روش استدلال و مناظره کن!
(سوره نحل، آیه ۱۲۵)
فصل 3 کتاب ریاضی نهم شامل پنج درس میباشد :
- درس اول : استدلال
- درس دوم : آشنایی با اثبات در هندسه
- درس سوم : همنهشتی مثلثها
- درس چهارم : حل مسئله در هندسه
- درس پنجم : شکلهای متشابه
استدلال
استدلال، یعنی دلیل آوردن و استفاده از دانستههای قبلی، برای معلوم کردن موضوعی که در ابتدا مجهول بوده است. در بسیاری از کارهای روزمره به استدلال نیاز پیدا میکنیم. راههای متفاوتی برای استدلال کردن هست که اعتبار و قابل اعتماد بودن آنها میتواند یکسان نباشد. به استدلالی که موضوع مورد نظر را به درستی نتیجه بدهد، اثبات میگوییم.
در کار در کلاس صفحه ۳۳ به موضوع مثال نقض پرداخته شده است و از دانشآموز میخواهد با آوردن مثلثی که یک زاویه باز (زاویه بیشتر از ۹۰ درجه و کمتر از ۱۸۰ درجه) دارد، نتیجه بگیرد که؛ در هر مثلث، محل برخورد ارتفاعها، همیشه درون مثلث نیست.
در فعالیت صفحه ۳۴ با آوردن شکلهای زیر مشاهده کردن و یا استفاده از سایر حواس پنجگانه برای اطمینان از درستی یک موضوع کافی نیست و رد میشود.
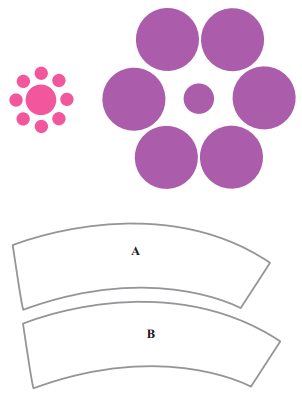
بنابراین، هرچند به طور معمول در ریاضیات و به ویژه در هندسه به کار بردن شکلها، ترسیم آنها و استفاده از شهود به تشخیص راهحلها و ارائه حدسهای درست کمک زیادی میکند، باید توجه کرد به تشخیصی که براساس این روشها بوده است، نمیتوانیم به طور کامل اطمینان کنیم.
در آخر این درس با آوردن چند سوال در تمرینات صفحه ۳۵ و ۳۶ کتاب درسی، از دانشآموزان خواسته شده است در مورد درستی استدلالها بحث کنند.
آشنایی با اثبات در هندسه
در درس اول یاد گرفتید که دیدن و استفاده از حواس و یا ارائه مثالهای متعدد و همچنین توجه به ابعاد ظاهری برای ایجاد اطمینان از درستی یک موضوع کفایت نمیکند و باید از دلیلهای منطقی و قانعکننده کمک گرفت و با استدلال، درستی آن موضوع را ثابت کرد. در روند استدلالمان از اطلاعات مسئله (فرض یا دادهها) و حقایق و اصولی که درستی آنها از قبل برای ما معلوم شده است برای رسیدن به خواسته مسئله (حکم) استفاده میکنیم.
اولین اقدامی که برای اثبات انجام میدهیم، تشخیص فرض، حکم و واقعیتهای مرتبط با آن مسئله است که از قبل آنها را میدانستیم. سوال بسیار مهم فعالیت صفحه ۳۸ که میخواهد اثبات کنید: قطرهای مستطیل، مساوی است، برای یادگیری بهتر تشخیص فرض، حکم و اثبات آنچه سوال خواسته است، آورده شده است.
بنابراین به طور کلی:
- فرض: اطلاعات و دادههای سوال یا دانستنیهای قبلی ما از یک موضوع درست است.
- حکم: خواسته مسئله یا آنچه سوال از ما میخواهد که اثباتش کنیم.
کار در کلاس صفحه ۳۸ با آوردن ۳ سوال میخواهد؛ فرض و حکم را برای مسئلههای داده شده را مشخص کنید. سپس در فعالیت و کار در کلاس صفحات ۳۹ و ۴۰ راه را برای استدلال کردن و رسیدن به پاسخ برای اثبات باز کرده است. اثبات سوال مهم زیر نیز در این رابطه است.
ثابت کنید هر نقطه روی عمودمنصف یک پارهخط (مثلا AB) از دو سر آن پارهخط (AB) به یک فاصله است.
موضوع تعمیم نیز بحث جدیدی برای پایه نهم است که در سالهای بعد کاربردیتر میشود و اشاره به این دارد:
وقتی خاصیتی را برای یک عضو از یک مجموعه ثابت کردیم، اگر تمام ویژگیهایی که در استدلال خود به کار بردهایم در سایر عضوهای آن مجموعه نیز باشد، میتوان درستی نتیجه را به همه عضوهای آن مجموعه تعمیم داد.
این درس شامل چند مسئله مهم دیگر نیز است:
- مجموع زاویههای داخلی مثلث °۱۸۰ است.
- زاویههای متقابل به رأس با هم برابر است.
- در هر مثلث، اندازهی زاویه خارجی با مجموع اندازههای دو زاویه داخلی غیرمجاور با آن برابر است. (سوال ۱ تمرین صفحه ۴۲)
- ثابت کنید هر نقطه که روی نیمساز زاویه قرار دارد از دو ضلع آن زاویه به یک فاصله است. (سوال ۴ تمرین صفحه ۴۳)
همنهشتی مثلثها
با مفهوم همنهشتی مثلثها در پایه هشتم آشنایی پیدا کردهاید. در کتاب ریاضی نهم به صورت جامع و کاربردی به آن پرداخته شده است. برای اثبات سوالات همنهشتی مثلثها باید دنبال ۳ دلیل (یا ۲ دلیل) بگردیم تا بتوانیم آنچه سؤال از ما میخواهد اثباتش کنیم.
همنهشتی مثلثها در حالت کلی:
- حالت اول: سه ضلع مساوی (ض ض ض)
- حالت دوم: دو ضلع برابر و یک زاویه مساوی بین آنها (ض ز ض)
- حالت سوم: دو زاویه برابر و یک ضلع مساوی بین آنها (ز ض ز)
دو حالت همنهشتی ویژه مثلثهای قائمالزاویه:
- حالت اول: وتر برابر و داشتن یک ضلع مساوی (و ض)
- حالت دوم: وتر برابر و داشتن یک زاویه ی تند (حاده) مساوی (و ز)
تمرینهای صفحه ۴۸ کتاب درسی ریاضی نهم، دانشآموز را برای اثبات مسائل همنهشتی مثلثها به خوبی آماده میکند.
حل مسئله در هندسه
برای حل مسائل هندسی، راهحل کلی وجود ندارد؛ اما میتوان مراحلی را مشخص کرد که برای هر مسئله هندسه، آنها را توصیه میکنند.
قدمهای حل مسئله
- صورت مسئله را به دقت بخوانید و مفاهیم تشکیل دهنده آن را بشناسید.
- اگر مسئله فاقد شکل است با توجه به صورت مسئله، یک شکل مناسب برای آن رسم کنید.
- دادههای مسئله (فرض) و خواستههای آن (حکم) را تشخیص داده و در یک جدول بنویسید.
- برای رسیدن از فرض به حکم راهحلی پیدا کنید. روشهای مختلفی برای اینکار هست که آنها را به مرور میآموزید.
همچنین برای مسائلی که اثبات (رسیدن به حکم) آنها بوسیله همهنشتی مثلثها ممکن است به طور خلاصه ۵ مرحله زیر پیشنهاد میشود:
قبل از حل تمرینهای صفحه ۵۱ و ۵۲ یک نکته (قضیه) مهم در صفحه ۵۰ آورده شده است که دانشآموزان عزیز باید به کمک مراحل بالا آن را اثبات کنند.
در یک دایره اگر دو کمان برابر باشند، وترهای نظیر آنها با هم برابرند و اگر دو وتر برابر باشند، کمانهای نظیر آنها نیز با هم برابرند.
شکلهای متشابه
کتاب با آوردن دو تصویر زیر، از دانشآموزان میخواهد تفاوت آنها را پیدا کنند و با این توصیف، شکلهای مثل هم را در ذهنشان تجسم میکند.

نتیجه: هرگاه در دو چندضلعی همه ضلعها به یک نسبت تغییر کرده باشد (کوچک یا بزرگ شده، و یا بدون تغییر باشد.) و اندازهی زاویهها تغییر نکرده باشد، آن دو چندضلعی با هم متشابهند. و به نسبت دو ضلع متناظر در دو شکل متشابه، نسبت تشابه میگویند.
تمرینهای صفحه ۵۷ و ۵۸ سعی کرده است هم به ارتباط تشابه با همنهشتی مثلثها بپردازد و هم با آوردن موضوع مقیاس در نقشه به نحوی کاربرد ریاضی با مسائل روزمره را بیان کرده است.
تعریفهای مورد نیاز این فصل:
- ارتفاع: خطی که از یک رأس بر ضلع مقابل یا امتداد آن عمود میشود.
- عمودمنصف: خطی که در مثلث بر یک ضلع عمود است و آن را نصف میکند.
- نیمساز: خطی که زاویه را به دو قسمت مساوی تقسیم میکند.
- میانه: خطی که از رأس به وسط ضلع مقابل وصل میشود.
.
.
.
آموزش مرتبط : فیلمهای آموزشی تدریس ریاضی نهم - فصل سوم (کلیک کنید...)
توجه: دانشآموزان عزیز توجه داشته باشید که برای یادگیری بهتر و موفق شدن در امتحان ریاضی پایه نهم بهتر است خودتان روی تمرینات و سوالات خوب فکر کنید و سعی کنید جوابی برای آنها پیدا کنید و در مرحله آخر سراغ جواب بروید. سریعا پاسخ را نگاه نکنید. ابتدا خودتان جوابی بنویسید و بعد راهحل درست را نگاه کنید.
.
.
دانلود PDF رایگان حلالمسائل ریاضی نهم فصل ۳
گردآورنده: دنیاها، دانشنامۀ فارسی | www.Donyaha.ir
![]()