لئونارد اویلر
لئونارد اویلر (به آلمانی: Leonhard Euler) ریاضی دانان و فیزیک دانان برجسته، در 15آوریل 1707 در شهر بازل سوئیس متولد شد پدرش از کشیشان پیروکالون بود و میل داشت پسرش جانشین او شود ولی اویلر بر خلاف میل او در دانشگاه بازل به مطالعه علوم الهی پرداخت پدر اویلر تعلیمات مقدماتی از جمله ریاضیات را به او داد اویلر بعداٌ چند سالی را در بازل به سر برد و در یکی از دبیرستانهای (گومنازیوم) نسبتاٌ در سطح پایین محلی به تحصیل پرداخت.
در دبیرستان ریاضیات اصلاٌ تدریس نمی شد و در نتیجه اویلر این دانش را به طور خصوصی نزد ریاضیدانی به نام یوهان بورکهارت آموخت در سال 1720 اویلر که هنوز 14 سال بیشتر نداشت وارد بخش ادب و هنر دانشگاه بازل شد تا پیش از کسب تخصص اطلاعات عمومی بیندوزد از جمله استادان او یوهان یکم برنوس بود که در کرسی ریاضیات جانشین برادرش یاکوب شده بود. اویلر در سال 1722 معادل درجه لیسانس در ادبیات را دریافت کرد و در 1723 در رشته فلسفه فوق لیسانس گرفت.
زندگی اویلر
در 18 سالگی پژوهشهای مستقل را آغاز کرد نخستین کار او یادداشت کوچکی بود در باره رسم منحنیهای همزمان در یک مقاله که در سال 1726 منتشر شد در پی آن در همان نشریه مقاله ای در باره مسیرهای متقابل جبری انتشار داد (1727) در پائیز 1726 از اویلر دعوت شد که به عنوان دستیار فیزیولوژی در سن پترزبورگ خدمت کند در 1727 از بازل به سن بترزبورگ رفت در آنجا بیدرنگ این بخت مساعد را یافت که در رشته واقعی خود کار کند و بعنوان عضو وابسته فرهنگستان دربخش ریاضیات منصوب شد.
در 1731 به استادی فیزیک رسید و در 1733 که دانیل برنولی به عنوان استاد ریاضیات به بازل برگشت، اویلر جانشین وی شد او از مرداد 1727 گزارشهایی در باره پژوهشهای خویش به جلسات فرهنگستان می فرستاد او آنها را در جلد دوم صورت جلسات فرهنگستان (گزارشهای فرهنگستان اپراتوری علوم یترو گراد) انتشار داد (سن پترزبورگ 1729) شهرت اویلر از 19 سالگی آغاز می گردد زیار در این سن بود که آکادمی پاریس حل مشکلی را در باره ساختمان دکل کشتی به مسابقه گذاشته بود و مقاله اویلر در این مورد مقام دوم را احراز نمود.
اویلر طی 14 سالی که در سن پترزبورگ بود به کشفهای درخشانی در زمینه هایی چون تحلیل ریاضی، نظریه اعداد و مکانیک دست یافت تا 1741 بین هشتاد تا نود اثر برای انتشار آماده کرده بود که 55 تای آنها از جمله دو جلد«مکانیک) را منتشر ساخت. اویلر در آن زمان عضو دو فرهنگستان سن پترزبورگ و برلین بود و سپس به عضویت انجم پادشاهی لندن (1749) و فرهنگستان علوم پاریس (1755) نیز انتخاب گردید در سال 1753 به عضویت انجمن فیزیک و ریاضیات بازل برگزیده شده بود.
اویلر در 1741 پس از 14 سال اقامت در روسیه به برلین رفت و 25 سال بعد را در آنجا سپری کرد او هنوز برای هر دو فرهنگستان برلین و سن پترزبورگ کار می کرد در تبدیل انجمن علوم سابق به یک فرهنگستان بزرگ که در سال 1744 رسماٌ با نام فرانسوی فرهنگستان پادشاهی علوم و ادبیات برلین بنیاد نهاده شد، فعالیت فراوان داشت طی این دوره اویلر به تنوع پژوهشهای خود بسیار افزود در همچشمی با دالامبر و دانیل برنولی دانش فیزیک ریاضی را پی ریزی کرد و در پیشبرد نظریه حرکت ماه و سیارات از رقیبان کلرو و دالامبر هر دو بود.
در همان زمان نظریه حرکت جامدات امکان ساخت ابزار ریاضی هیدرودینامیک را فراهم آورد هندسه دیفرانسیل سطوح را ابداع کرد و به شدت در باره نورشناسی برق و مغناطیس به پژوهش پرداخت همچنین در باره مسائل فن آوری نظیر ساختن دوربینهای شکستنی بیرنگ، تکمیل توربین آبی زگنر و نظریه چرخهای دندانه دار به تفکر پرداخت.
شمار آثار اویلر در دوره اقامت در برلین از 380 کمتر نبود که از میان 275 اثر انتشار یافتند از جمله تعدادی کتابهای مفصل تکنگاشتی در باره حساب جامع و فاضل تغییرات، کتابی بنیادین در باره محاسبه مدارهای اجرام آسمانی کتابی در باره توپخانه و پرتاب گلوله کتاب مدخلی به تحلیل نامتناهی رساله ای در کشتی سازی و دریانوردی که صورت آغازین آن در سن پترزبورگ تهیه شده بود.
نخستین نظریه او در باره حرکت ماه و اصول حساب دیفرانسیل سه کتاب آخر به هزینه فرهنگستان سن پترزبورگ انتشار یافتند و در آخر رساله ای بود در باره مکانیک جامدات به نام«نظریه حرکت اجسام جامد)(1756) رساله مشهور ( نامه هایی به یک شاهزاده خانم آلمانی در باره موضوعهای مختلف فیزیک و فلسفه) که در واقع درسهایی بود که اویلر به یکی از بستگان پادشاه پروس داده بود، تا پیش از بازگشت اویلر به سن پترزبورگ انتشار نیافتند این کتاب موفقیتی بی نظیر یافت و 12 بار به زبان اصلی تجدید چاپ گردید و به بسیاری زبانهای دیگر نیز ترجمه شد.
امضای لئونارد اویلر
نظریات اویلر
اویلر همچنان به مطالعات ریاضی خود ادامه می داد و رفقایش او را روح آنالیز ریاضی می دانستند. آراگو درباره اویلر چنین گفته است: اویلر با همان سهولتی که انسان نفس می کشد محاسبات ریاضی را انجام می دهد.
اویلر به معنای گسترده ای که در سده هجدهم برای کلمه هندسه کار می رفت هندسه دان بود در کار او ریاضیات بستگی نزدیکی با کاربرد سایر علوم با مسائل فناوری و با زندگی عمومی داشت در آثار ریاضی اویلر تحلیل ریاضی جایگاه نخست را دارد هفده جلد از (مجموعه آثار) او در این زمینه است. او با کشفیات خاص متعدد به تحلیل ریاضی یاری داد. نحوه عرضه آن در کتابهای درسی خود را منظم ساخت در بنیادگذاری رشته های متعدد ریاضی نظیر حساب جامع و فاضل تغییرات، نظریه معادلات دیفرانسیل، نظریه مقدماتی توابع متغیرهای مختلط و نظریه توابع خاص بی اندزه کمک کرد اویلر بسیاری از قراردادهای کنونی علائم ریاضی را وارد میدان کرد.
اویلر با حل مسئله پل‌های کونیگزبرگ علم گراف و گرایشهای مهمی از آن مثل توپولوژی را به وجود آورد.در تئوری اعداد هم که توابعی چون فی اویلر و قضیه اویلر در مورد اعداد اول (تعمیمی بر قضیه ی کوچک فرما) به نام او ثبت شده اند و در جبر نیز اتحاد ها و روش هایی به او منسوب است. خط اویلر (خطی که مرکز ارتفاعی و گرانیگاه و مرکز دایره محیطی مثلث بر آن واقعند) هم یادگاری از این ریاضیدان بزرگ در هندسه اقلیدسی است.
اویلر در سال ۱۷۳۵، راه‌حلی برای مسئله‌ی مشهور پل‌های کونیگسبرگ ارائه کرد. شهر کونیگسبرگ در پادشاهی پروس (آلمان) روی رودخانه‌ی پلگوریا واقع شده و از دو جزیره تشکیل می‌شد. این دو جزیره به‌وسیله‌ی ۷ پل به هم متصل بودند. مسئله‌ی مشهور این شهر می‌گفت آیا می‌توان مسیری را پیدا کرد که تنها با یک بار عبور کردن از روی هر پل، تمامی پل‌ها را طی کرده و به نقطه‌ی اول بازگشت. پاسخ این مسئله، منفی است. تحلیل این مسئله، مفهومی را به‌نام دور اویلری، به هندسه افزود.
نمایی از شهر کونیگسبرگ و ۷ پل معروف آن
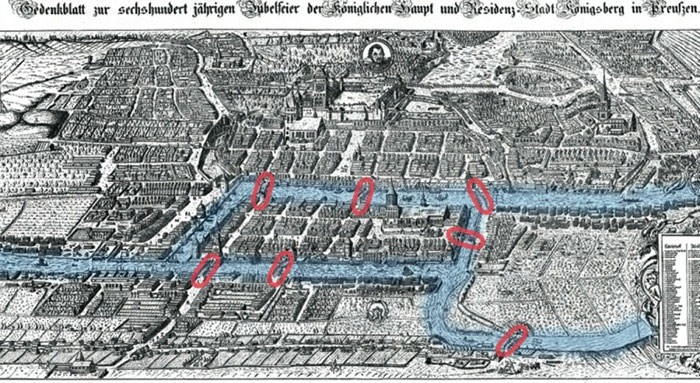
دور اویلری یا پاسخ مسئله‌ی کونیگسبرگ، اولین قضیه در نظریه‌ی گراف بود. در نتبجه‌ی پیشرفت بیشتر در این مسئله، اویلر مسئال توپولوژیکی را نیز با محاسبات خود مورد بررسی قرار داد و مفهومی با نام مشخصه اویلر به ریاضیات و هندسه اضافه شد. مطالعه‌ی این مفهوم و همچنین پیشرفت دادن آن توسط بزرگانی همچون آگوستین لویی کوشی، علم توپولوژی را ایجاد کرد.
اویلر تاثیر زیادی در پیشرفت مطالعه‌ی هندسه‌ی تحلیلی و مثلثات داشت. جالب است بدانید اویلر اولین کسی است که سینوس و کسینوس را به‌عنوان توابع ریاضیاتی معرفی کرد. پیش از او، بطلمیوس آنها را به‌عنوان وترهایی از دایره توصیف کرده بود.
عبارت و شرح ریاضی فرمول مشهور اویلر در مثلثات
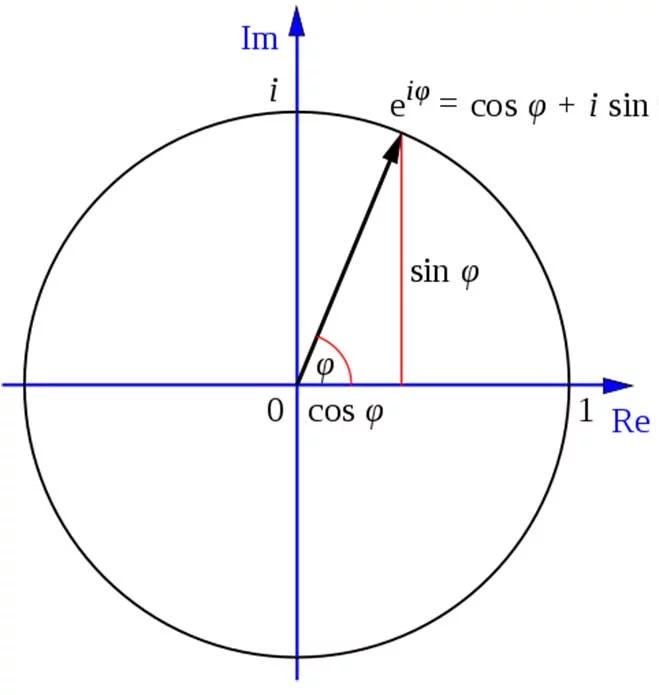
همان‌طور که گفته شد، نقش این دانشمند بزرگ در پیشرفت هندسه، حسابان و تئوری اعداد، غیرقابل توصیف است. او با استفاده از آنالیز ریاضی، محاسبات دیفرانسلی لایبنیتس را روش نیوتن در محاسبه‌ی فاصله‌ها ترکیب کرد. او توابع بتا و گاما و همچنین فاکتور انتگرالی برای محاسبات دیفرانسلی را به دنیا معرفی کرد.
مکانیک پیوسته، نظریه‌ی حرکت ماه الکسی کلرو، مسئله‌ی سه جسم، الاستیک، آکوستیک، نظریه‌ی موجی نور، هیدرولیک و موسیقی، از زمینه‌های مطالعاتی لئونارد اویلر بودند. بنیان‌گذاری مفاهیم مکانیک تحلیلی نیز از دیگر دستاوردهای بزرگ این دانشمند سوئیسی است. او در سال ۱۷۳۴، مفهوم f را برای توابع معرفی کرد. علامت e برای ریشه‌ی لگاریتم طبیعی، علامت i برای جذر دوم عدد ۱-، علامت Π برای عدد پی، Σ برای محاسبه‌ی سری‌ها و علامت Δy در محاسبات دیفرانسیل، از یادگارهای این ریاضیدان هستند.
ریاضیات کاربردی
یکی از شاخه‌های مهم مطالعات اویلر، به پیاده‌سازی تحلیل‌های عددی و محاسبات عددی در حل مسائل واقعی جهان مربوط است. او از انواع ابزارها هچون اعداد برنولی، سری‌های فوریه و اعداد اویلر و همچنین انواع انتگرال‌ها برای حل این مسائل استفاده می‌کرد. در نهایت، این دانشمند نقش بزرگی در استفاده از ریاضیات برای حل مسائل فیزیکی داشت.
اویلر از مفاهیم ریاضی در موسیقی نیز استفاده می‌کرد. او در سال ۱۷۳۹ مقاله‌ای با عنوان Tentamen novae theoriae musicae منتشر کرد و در آن، به توضیح نظریه‌‌های موسیقی در ریاضیات پرداخت. البته این بخش از تحقیقات او، شهرت زیادی پیدا نکرد. کارشناسان، این مقاله را برای موسیقی‌دانان، بیش از حد ریاضیاتی و برای ریاضی‌دانان بیش از حد موسیقایی می‌دانند.
فیزیک و نجوم
اویلر در توسعه‌ی نظریه‌ی پرتو اویلر برنولی نقش داشت که امروزه به‌عنوان سنگ بنای مهندسی شناخته می‌شود. در واقع اویلر علاوه بر پیاده‌سازی فرمول‌ها در مسائل مکانیک کلاسیک، از آنها در حل مسائل نجومی و آسمانی نیز استفاده کرد. او با این ابزارها توانست مدار دقیق ستاره‌های دنباله‌دار و دیگر اجرام آسمانتی را محاسبه کند. در نتیجه‌ی تحقیقات او، توسعه‌ی جداول دقیق عرض جغرافیایی نیز انجام شد.
مثالی از شرح مجموعه‌ها با نمودار اویلر
مطالعات اویلر در زمینه‌ی اپتیک نیز نتایج قابل توجهی داشته است. او با نظریه‌ی نیوتن در مورد نور به‌عنوان ذره مخالف بود. او در مقاله‌های خود در دهه‌ی ۱۷۴۰ با جدیت به این موضوع پرداخت تا در نهایت، نظریه‌ی نور به‌عنوان موج که توسط کریستیان هویگنس ارائه شده بود، به‌عنوان نظریه‌ی غالب پذیرفته شود. البته این نظریه تا زمان اثبات نظریه‌ی کوانتومی نور پابرجا بود.
منطق اویلری
اویلر در استفاده از منحنیهای بسته در اثبات قیاس منطقی مشهور بود. این دیاگرام‌ها به‌عنوان دیاگرام اویلر مشهور شدند. این نمودارها بعدا با نام نمودارهای ون به شهرت رسیدند. نمودارهای اویلر یا ون، برای نشان دادن مجموعه‌های ریاضی، هم‌پوشانی و ارتباط آنها با یکدیگر و همچنین زیرمجموعه‌ها به کار می‌روند.
فعالیت اویلر در نقشه‌کشی نیز قابل توجه بود. او در پروژه‌ای دولتی روی این مسئله تمرکز داشت و به Delisle کمک کرد تا یخک نقشه از امپراطوری روسیه آماده کند. این نقشه با نام اطلس روسیه آماده و در سال ۱۷۴۵ به نمایش عمومی گذاشته شد. نقشه‌ی نهایی، از ۲۰ نقشه‌ی کوچک ساخته شده بود.
کتابها و مقالات
کشفهایی که در نیمه سده هجدهم در زمینه تحلیل ریاضی انجام گرفته بود به شیوه ای منظم بوسیله اویلر در دوره سه کتابی زیر خلاصه شده است:
- مدخلی بر تحلیل نامتناهی (1748)
- روشهای حساب دیفرانسیل (1755)
- روشهای حساب انتگرال (1768 – 1770)
او هر روز اکتشافی به اکتشافات خود می افزود و تعدا آنها آنقدر زیاد است که حتی امروزه موفق به چاپ کامل آثار او نگردیده اند در همین اوقات بود که مسئله ای از طرف آکادمی مطرح شد و اویلر در عرض سه روز آن را حل کرد و مریض شد. در این بیماری یک چشم خود را از دست داد در 60 سالگی بود که بدبختی عجیبی به او روی کرد و آن از دست دادن چشم دیگرش بود گر چه چشم او را با موفقیت عمل کردند ولی زخم آن دچار عفونت شد و برای همیشه چشمان خود را از دست داد. اویلر مردی که از تندخویی و حسادت به کنار بود در 18 سپتامبر 1783 هنگامی که مشغول محاسبه مسیر سیاره اورانوس بود ناگهان با گفتن کلمه «من مردم» زندگی را بدرود گفت.
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
