: دسته: بیوگرافی; بازدید: 513

ژاکوب برنولی

ژاکوب برنولی (زاده ۲۷ دسامبر۱۶۵۴ میلادی در شهر بازل- در گذشته ۱۶ اوت ۱705 میلادی) ریاضی دان و فیزیکدان سوییسی بود.
سوییس پدر ژاکوب برنولی، نیکولاس برنولی (1623-1708) ادویه چی بودن را از پدرش به ارث برده بود. کارش در آمستردام و بعدها در باسل توسط پدرش مدیریت می شد.
خانواده اش از دست اذیت های حاکمان اسپانیایی هلند، به منطقه بلژیک پناه برده بودند. فیلیپ (پادشاه اسپانیا) دوک آلبا را در سال 1567 با یک ارتش بزرگ برای سرکوبی مخالفان قانون اسپانیایی و برای تحمیل کاتولیک رومی به مردم همچنین گماردن مامورانش به هلند فرستاد.

آلبا انجمن تروبلس را که به صورت دادگاه بود برپا کرد. این دادگاه بیش از 12000 نفر را محکوم کرد و البته خانواده هایی (مانند خانواده برنولی) که بر آیین پروتستان بودند از کشور گریختند.

زندگی ژاکوب

نیکولاس برنولی بواسطه عضویت درانجمن شهروند مهمی به حساب می آمد. مادر ژاکوب برنولی هم اصالتاً از یک خانواده باسلی مهم بود که بانکداری می کردند و عضو انجمن های محلی بودند. ژاکوب برنولی برادر یوهان برنولی و عموی دانیل برنولی بود. والدینش او را مجبور کرده بودند که فلسفه والهیات بخواند که به شدت او را ناراحت می کرد. با این وجود او با درجه عالی از دانشگاه باسل در رشته فلسفه در سال 1671 فارغ التحصیل شد و لیسانس الهیات را در سال 1676 اخذ کرد. در مدتی که ژاکوب برنولی مدارج دانشگاهیش را می گرفت مشغول مطالعه ریاضیات و نجوم بود. البته این عمل او موافق طبع پدر و مادرش نبود. شایان ذکر است که او نمونه معمولی از خانواده برنولی بود که علیرغم فشار زیاد برای انجام کار در سایر رشته ها، رشته ریاضیات را مطالعه کرد. با این حال ژاکوب برنولی برای اولین بار در این راه قدم گذاشت و در واقع این زمینه برای او کمی متفاوت بود.

چون قبل از او هیچ کس از خانواده برنولی ها ریاضیات را انتخاب نکرد. بعدها اعضای خانواده برنولی بیشتر تحت تأثیر این سنت مطالعه ریاضیات و فیزیک ریاضی قرار گرفتند. در سال 1676 (بعد از دریافت مدرک الهیات) برنولی به ژنو نقل مکان کرد و در آنجا به عنوان مربی مشغول به کار شد. او سپس با گذراندن مطالعه دو ساله همراه با مریدان دسکارتز که در آن زمان توسط مالبرانچ راهنمایی می شدند به فرانسه سفرکرد. او در سال 1685 به هلند سفرکرد و ریاضیدانان زیادی را ملاقات کرد که یکی از آنها هاد (Hudde) بود. او در حالی که مطالعاتش را همراه با سرشناس ترین ریاضی دانان و دانشمندان اروپا ادامه می داد به انگلستان سفر کرد و در بین بقیه بویل و هوک را ملاقات کرد. در این زمان او به شدت مجذوب نجوم بود و کاری کرد که حاصلش تئوری نه جندان دقیق در مورد ستارگان دنباله دار بود. نتیجه سفرهای برنولی این بود که شروع به تطبیق با ریاضیدانانی بکند که سالیان زیادی اینکار را کرده بودند.
ژاکوب برنولی درسال 1683 به سوییس برگشت و مشغول تدریس مکانیک در باسل شد. سخنرانی های مهمی در زمینه مکانیک جامد و مایع ایراد کرد. با وجود اینکه مدرک برنولی الهیات بود و طبیعتاً باید به کلیسا برمی گشت ولی او این مدرک را نادیده گرفت. عشق واقعی او به ریاضیات وفیزیک تئوریک بود و این موارد، زمینه هایی بودند که او درباره آنها سخنرانی و تحقیق می کرد.
در طول این مدت او آثار برجسته ریاضیات شامل موارد هندسه دسکارتز و ون شوتن را از روی نسخه لاتین مطالعه می کرد. ژاکوب برنولی همچنین آثار Wallis و Barrow را مطالعه کرد و مشتاق هندسه ریز (هندسه خرد) شد. ژاکوب شروع به نوشتن و انتشار در مجله ActaEruditorum شد که در سال 1682 در lapzig چاپ و منتشر می شد.

ازدواج ژاکوب برنولی

در سال 1682 ژاکوب برنولی با جودیس استپانوس ازدواج کرد. آنها صاحب دو فرزند شدند. یک پسر بچه که نام پدربزرگش نیکولاس را بر او گذاشتند و یک دختر بچه. این بچه ها برخلاف خانواده برنولی به تحصیل ریاضیات و فیزیک ادامه ندادند.

رابطه ی برادری

یکی از مهم ترین اتفاقات مطالعات ریاضی برنولی زمانی اتفاق افتاد که برادر کوچکترش (یوهان برنولی) شروع به کار در زمینه ریاضیات کرد، یوهان توسط پدرش توصیه به مطالعه پزشکی شده بود اما او از برادرش خواهش کرد که به او ریاضیات بیاموزد. ژاکوب برنولی در سال 1687 پروفسور ریاضیات درباسل شناخته شده بود و دو برادر شروع به مطالعه محاسباتی کردند. همانطور که لایبنیز در سال 1684 طی مقاله ای درباره محاسبات دیفرانسیلی Nova Methods Pro Maximis et Minimis… در مجله Acta Eruditorum آورده است. آنها همچنین آثار Von Tschirnhaus را مطالعه کردند. اینکه آثار لایب نیتز درمورد محاسبات ریاضی بسیار سردرگم و گنگ بود کاملاً واضح است که برنولی ها اولین افرادی بودند که برای درک و کاربرد این تئوری ها سعی کردند.
علیرغم اینکه ژاکوب و یوهان هر دو در یک زمینه مشابه کار می کردند اما رابطه آنها از یک همکار به یک رقیب تبدیل شد. خودستایی های یوهان برنولی باعث شد که ژاکوب به وی بتوپد. ژاکوب نوشته بود که یوهان مثل شاگرد اوست و تمام دستاورد او درواقع تکرار چیزهایی است که ژاکوب به او یاد داده است، البته این کاملاً ناعادلانه بود. ژاکوب مخصوصاً بعد از سال 1697 طی یک چاپ که بدنام کننده و در یک قالب غیر ضروری بود، به تاختن به برادرش ادامه داد. با این وجود ژاکوب انتقاد در ملأ عام را ترک نکرد. او از پرسنل دانشگاه ایراد می گرفت و دوباره بیانات انتقادآمیز ایراد می کرد(همانطور که انتظار می رفت) برادرش را در شرایط سخت دانشگاه ترک کرد.

شاید ژاکوب احساس کرده بود که یوهان ریاضی دان قویتری ازاوست و چون ذاتاً انتظار تحسین از دیگران داشت این احساس او را اذیت می کرد. همانطور که هافمن در نوشته هایش آورده است.

حساسیت، بدخلقی، ولع متقابل برای انتقاد، تمایل زیاد دو برادر در نشان دادن این بیگانگی بین دو برادر واضح بود. گرچه ژاکوب ملایم تربود وخردمندانه عمل می کرد.
همانطور که در اینجا آمده است هر دو برادر در بگو مگو کردن به یک اندازه مقصر بودند، یوهان سمت استادی ریاضیات باسل را می خواست اما ژاکوب این کرسی را برای خود حفظ می کرد و مطمئناً از اینکه آخر سر مجبور شد در سال 1695 به هلند نقل مکان کند ناراحت و سرخورده بود، این در واقع فاکتور مکمل در به هم خوردن رابطه بین دو برادر در سال 1697 بود.

البته مشاجره دو برادر نشان دهنده حماقت خاص آنها بود. زیرا هر دو برای علم ریاضیات جانفشانی می کردند که خیلی با اهمیت تر بود، اینکه رقابت بین آن دو آنها را به موضوعات بزرگتری سوق می داد یا در صورت ادامه همکاری آنها به دستاوردهای بزرگتری می رسیدند قابل تشخیص نیست. ما اکنون به بررسی چند کار ژاکوب برنولی در پیشرفت مراحل مهم ریاضیات لایب نیتز در محاسبات می پردازیم.

کارهای برنولی

نخستین اثر ژاکوب برنولی انتشار جزوه ای در مورد منطق و جبر موازی در سال 1685، احتمالات در سال 1685، هندسه در سال 1687 بود. نتیجه هندسه او یک ساختار را به دست می داد که توسط دو خط عمود بر هم می توان یک مثلث را به چهار بخش مساوی تقسیم کرد. او در سال 1689 اثر مهمی در سری های نامتناهی و قاعده اعداد بزرگ در تئوری احتمالات را منتشر کرد، تعبیر احتمالات به عنوان فرکانس نسبی بیانگر آن است که اگر آزمایشی را به دفعات زیادی انجام دهیم آنگاه فرکانس نسبی با هر رخداد برابر با احتمال وقوع ان رخداد است. قاعده اعداد بزرگ تعبیر ریاضی از این نتیجه است. ژاکوب برنولی طی سال های 1682 تا 1704، پنج رساله درمورد سری های نامجدود ارائه کرد. دو رساله حاوی نتایج ارزشمندی از قبیل پایه و اساس اینکه همگراست، بود. گرچه اعتقاد برنولی جدید بود ولی طی چهل سال بعد توسط Mengoli اثبات شد. برنولی نتوانست فرم بسته ای برای پیدا کند. اما نشان داد که این سری باید به یک عدد کمتر از دو همگرا باشد. اویلر اولین کسی بود که حاصل جمع این سری را در سال 1737 پیدا کرد. او همچنین سری های توانی را مورد مطالعه قرار داد و از آزمایش آنها به خیلی چیزهای مرکب علاقه پیدا کرد.

او در می سال 1690 طی مقاله چاپ شده در Acta Eruditorum نشان داد که برای حل مسئله تعیین ایزوکرون (isochrone) باید یک معادله دیفرانسیل غیر خطی درجه یک را حل کرد. ایزوکرون یا منحنی با شیب ثابت، منحنی حرکت (نزول) یک ذره از نقطه نا مشخص تا کف تحت نیروی گرانش است که نقطه شروع حرکت مهم نیست. این موضوع در سال 1687 توسط Huygens و در سال 1689 توسط لایبنیز مورد مطالعه قرار گرفته است. پس از پیدا کردن معادله دیفرانسیل برنولی آن را با روش تفکیک متغیرها حل کرد، مقاله ژاکوب برنولی در تاریخ محاسبات و در سال 1690 از آنجا که علامت انتگرال با مفهوم جمع کننده برای اولین بار آمده بود مهم و باارزش است. در سال 1696 برنولی معادله ای که امروز به معادله برنولی معروف است را حل کرد.
و هافمن این بخش از کار او را چنین توضیح داد:

کار حیاتی و دقیق برنولی روی مسایل قدیمی همانند آثار همزمان او روی ریاضیات نامحدود و همچنین پشتکار و قابلیت تحلیل او بر روی مسایل خاص مرتبط با هم حتی از نوع مکانیکی و دینامیکی ثابت شده است.

ژاکوب برنولی همچنین یک متد اصلی برای تعیین محاسبه منحنی از روی شیب دوایر انحنای آن پیدا کرد. او همچنین منحنی هایخورنده و منحنی های مرتبط با پارابولا ،به پیچه های لگاریتمی و epicycloids around را در سال 1692 مورد مطالعه و تحقیق قرار داد. Lemniscate Bernoulli اولین بار توسط برنولی در سال 1694مطالعه شد. در سال 1695 مسئله پل را مورد مطالعه قرار داد و از مطالعاتش در مورد منحنی های آن دریافت که وزن سرخورنده بر روی کابل های پل همواره پل را در حالت متعادل نگه می دارد.

اغلب کارهای ژاکوب برنولی در Ars Conjectandi بود که سال 1713(هشت سال پس از مرگ وی) منتشر شد. این کارش در هنگام مرگ او ناتمام بود اما هنوز هم یک مفهوم بزرگ در تئوری احتمالات است. برنولی آثار سایرین در مورد احتمالات را در کتابها خواند، مخصوصاً آثار van Schooten و لایبنیز و Prestet را مطالعه کرد. اعداد برنولی در کتابی پیرامون سری های نمایی آمده است. مثال های زیادی درمورد احتمال برد در بازی های مختلف در آن کتاب آمده است. مطالب جالب زیاد در مورد احتمالات وجود دارد:
.... احتمال مثل درجه قابل اندازه گیری از اطمینان، ضرورت و شانس، یک توقع متقابل ریاضی، یک قیاس از احتمال استقرایی، انتظار پیروزی است، وقتی که بازیکن ها برحسب چیره دست بودن تقسیم شوند در نظر گرفتن کلیه استدلالها و ارزش آنها و محایبات قابل تعیین آنهاست. اعداد بزرگ....

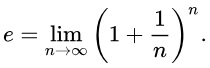
نامساوی برنولی

بسیاری از نامساوی‌های مطرح در ریاضیات برمبنای نامساوی برنولی اثبات یا نوشته شده‌اند. برنولی سعی داشت به کمک یک رابطه ریاضی، کران بالایی برای معادله ساده بسازد.

در آنالیز حقیقی، نابرابری برنولی نابرابری ای است که توان های 1 + x را تخمین می زند.

این نابرابری بیان می کند که برای هر عدد صحیح مانند r که r ≥ 0 و هر عدد حقیقی مانند x که x ≥ −1 داریم:

اگر r زوج باشد آنگاه نابرابری برای تمام اعداد حقیقی x برقرار است.

از نابرابری برنولی معمولاً به عنوان یک پله مهم در اثبات دیگر نابرابری ها در ریاضیات استفاده می شود. خود این نابرابری نیز را می توان به کمک استقرای ریاضی اثبات کرد.

هافمن دستاوردهای ژاکوب برنولی را این چنین جمع بندی کرده است:

برنولی پیشرفت بزرگی در جبر، در محاسبات بینهایت کوچک و در محاسبات متغیرها، مکانیک وتئوری سریها و تئوری احتمالات ایجاد کرد.او فردی خود رأی، کله شق، کینه جو، پست و شدیداً راضی از قابلیت های خود بود.با وجود این شخصیت او مجبور به قطع رابطه با برادر مستعد خودبود.اوبعدها هم همان شرایط را به کار برد.
برنولی یکی ازمهم ترین پایه گذاران متدهای رسمی در آنالیزهای درجه بالا بود. زیرکی و ریزه کاری به ندرت در متدهایش و آزمایشاتش دیده می شود. اما نهایت امانت و درستی در کارهایش به چشم می خورد.

مرگ او

ژاکوب برنولی در ۱۶ اوت ۱705 میلادی در حالیکه از بیماری سل رنج می برد،درگذشت.
ژاکوب برنولی تا مرگ خویش کرسی ریاضیات باسل را دراختیار داشت تا اینکه بعد از مرگش برادر او یوهان آن را تصاحب کرد، ژاکوب همچنین خواص پیچه های لگاریتمی را پیدا کرد که تقریباً جادویی هستند. او تقاضا کرده بود روی سنگ قبرش عبارت «من باید برخیزم که نظر قبلی ام عوض شده است» حک شود.

گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir