زندگی نامه جان نپر - کاشف لگاریتم

جان نپر ریاضی‏‎دان و نویسنده دینی اهل اسکاتلند بود که مفهوم لگاریتم را ابداع و پایه‌ریزی کرد. وی در سال ۱۵۹۴ کار بر روی مبحث لگاریتم‌ها را آغاز کرد. از دیگر کارهای او در ریاضیات، عدد نپر است.

او همچنین «استخوان‌های نپر» را اختراع کرد و دیگر اینکه علامت اعشاری را در حساب و ریاضیات رایج کرد.

زندگی

جان نپر در سال ۱۵۵۰ در مرکیستون کسل، در خانواده‌‏ای مرفه به دنیا آمد و به رسوم اشرافی انگلستان تربیت یافت. پدرش، ارچیبالد نپر، هفتمین لیرد مرکیستون و مادرش، جنت باثول، دختر یک سیاستمدار و قاضی بود.

اطلاعاتی درباره به تحصیلات ابتدایی جان نپر وجود ندارد؛ اما بسیاری بر این باورند که او به طور خصوصی در خانه آموزش داده می‌شد. در 13 سالگی، او در کالج سنت سالواتور، در سنت اندروز ثبت نام کرد. در دوران تحصیل او، کیفیت آموزش در دانشگاه پایین بود، که تا حدودی به دلیل ایجاد نزاع بین مذهبی‌های قدیمی و پروتستان‌ها بود. هیچ مدرکی از به پایان رساندن تحصیلات توسط نپر در سنت اندروز وجود ندارد. این اعتقاد وجود دارد که او به توصیه دایی‌اش برای ادامه تحصیل به سرزمین‌های اصلی اروپا مهاجرت کرد. توصیه داییش، آدام بوثول، در نامه‌ای که در 5م دسامبر 1560 به پدر نپر بود، نوشته شده:

«خواهش می‌کنم جناب، جان را به مدرسه‌ای در فرانسه یا فلاندر بفرستید زیرا او نمی‌تواند در خانه چیزی بیاموزد»

مشخص نیست که در اروپا در چه دانشگاهی درس خواند ولی وقتی در سال 1571 به اسکاتلند برگشت به زبان یونانی مسلط بود، زبانی که با آن در آن زمان، به طور معمول در دانشگاه‌های اروپا تدریس نمی‌شد؛ همچنین هیچ مدرکی مبنی بر ثبت نام وی در دانشگاه‌های برتر پاریس یا ژنو در این مدت وجود ندارد.

در سال 1571، نپر 21 ساله به اسکاتلند بازگشت و در سال 1574 یک قلعه در گارتنس خرید. پس از مرگ پدرش در 1608نپر و خانواده‌اش به قلعه مارکیستون کوچ کردند، جایی که باقی عمرش را در آن گذراند. او همچنین مالک یک ملک در شهر ادینبرگ بود.

اعتقادات و پیش‌بینی‌ها

وی در دوران جوانی، زمانی که اروپا دستخوش مناقشات دینی بود و نهضت پروتستانْ سراسر این قاره را در برگرفته بود، سفرهای زیادی به کشورهای اروپایى نمود و به مذهب پروتستانْ گرایید.

در سال 1593 ادعا نامه‌ای تند و پرخواننده‌ای علیه کلیسای رم تحت عنوان (کشف ساده ای از کلیه مکاشفات یوحنای قدیس) منتشر، و سعی کرد ثابت کند که پاپ ضد مسیح است. کتاب 21 بار به چاپ رسید، که حداقل 10 بار آن در دوران حیات مؤلف بود و نپر باور داشت که شهرت وی در بین نسل‌های بعدی بر مبنای این کتاب خواهد بود.

نپر همچنین پیشگویانه از پیداش ماشین‌های جهنمی جنگی گوناگونی نام برده که طرح‌ها و نمودارهایی با نوشته‌هایش همراه بود، وی پیشگویی کرد که در آینده آتشباری به وجود می‌آید که قادر به پاکسازی میدانی به محیط 4 مایل از هر موجود زنده‌ای با بیش از یک پا بلندی خواهد بود و ابزارهای دریانوردی زیر آب و ارابه‌ای با پوزه جانداری ساخته از آهن به عرصه می‌آیند که بر هر سو مرگ می‌پراکند. در جنگ جهانی اول این پیشگویی‌ها به ترتیب در وجود مسلسل، زیر دریایی و تانک نظامی تحقق پیدا کردند.

شگفت آور نیست که نبوغ و قدرت تجسم نپر بعضی‌ها را بر آن داشت تا  وی را از لحاظ فکری نامتعادل پندارند و برخی دیگر به او به عنوان رواج دهنده سحر و جادو نگاه کنند. داستان‌های بسیار و احتمالا بی‌پایه‌ای، در تایید این نظریات گفته می‌شوند. زمانی وی اعلام کرد که خروس سیاه زغالی او برای وی مشخص خواهد کرد که کدامیک از خدمتکارانش از او دزدی می‌کند. خدمتکاران یک به یک به اتاق تاریکی فرستاده شده بودند، با این دستور که پشت خروس را نوازش کنند. بدون اطلاع خدمتکاران، نپر پشت خروس را به دوده چراغ آغشته کرده بود، و خدمتکار مجرم، در بیم از دست زدن به خروس، با دست‌های تمیز بازگشته بود.

مورد دیگری نیز وقتی بود که نپر از دست کبوترهای همسایه که حبوبات او را می‌خوردند، به تنگ آمده بود. وی تهدید کرد در صورتی که همسایه‌اش جلوی پرواز این پرندگان را نگیرد، آنها را ضبط خواهد کرد. همسایه، با این تصور که گرفتن کبوترهایش عملا غیر ممکن است، به نپر گفت که وی مخیر است آنها را بگیرد. روز بعد همسایه شگفت زده کبوترهای خود را تلو تلو خوران روی چمن نپر مشاهده می‌کند که نپر با خونسردی آنها را در کیسه‌ای می‌ریخته است. نپر پرندگان را با پاشیدن نخود فرنگی‌های آلوده به شراب پیرامون چمن خود مست کرده بوده است.

شهرت

شهرت عمده نپر در ریاضیات مبتنی بر طریقه تازه‏‌ای بود که وی برای انجام عملیات محاسباتی عرضه داشت. وی معتقد بود که کلیه اعداد را می‏‌توان به صورت بالقوه نوشت. مثلاً چهار را به صورت دو به توان دو. او هم‏چنین بر این اعتقاد بود که اگر اعداد به این صورت نوشته شود، عمل جمع، جانشین ضرب و عمل تفریق جانشین تقسیم خواهد شد. نپر برای تحقق بخشیدن به فکر خود، مدت بیست سال وقت صرف کرد و توانست فرمول‏‌های پیچیده‏‌ای برای نوشتن کلیه اعداد به صورت بالقوه به دست آورد. وی این نحوه محاسبه را لُگاریتم به معنای اعداد متناسب نامید.می‌‏توان گفت که تأثیر این یافته‌‏های علمی در علم آن روز، با تأثیر ماشین‏‌های حسابگر امروزی برابر است.

نپر در ریاضیات، عدد نپر را معرفی کرد است و با ابداع علامت اعشاری، کسر اعشاری را به صورت امروزی درآورد.

کارهای او

نپر برای رهایی از مناقشات سیاسی و مذهبی خود را با مطالعه ریاضیات و علوم سرگرم می‌کرد و نتیجه‌اش ۴ موضوع زیر است که ثمره نبوغ اوست و در تاریخ ریاضیات ثبت شده ا ست :

• اختراع لگاریتم
• یادآور زیرکانه‌ای، موسوم به قاعده اجزاء مستدیر، برای به دست آوردن دوباره فرمول‌هایی که در حل مثلث‌های قائم‌الزاویه کروی به کار می‌روند.
• حداقل دو فرمول مثلثاتی از یک گروه چهارتایی معروف به مشابهات نپر که در حل مثلث‌های غیر مشخص کروی مفیدند.
• اختراع اسبابی موسوم به میله‌های نپر یا استخوان‌های نپر، مفید در ضرب، تقسیم، واستخراج ریشه‌های دوم اعداد به طور مکانیکی.

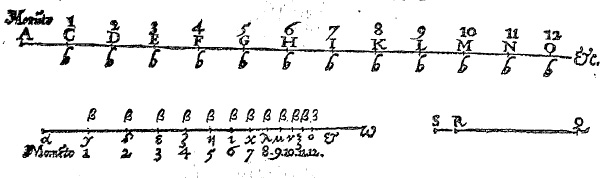
نپر بحث خود درباره لگاریتم‌ها را در 1614 در رساله‌ای تحت عنوان شرح قانون شگفت‌انگیز لگاریتم‌ها منتشر کرد. این اثر حاوی جدولی ا ست که لگاریتم سینوس زوایا را برای دقیقه‌های متوالی یک کمان می‌دهد. رساله توجه فوری و گسترده‌ای را برانگیخت، و در سال بعد از انتشار آن هنری بریگز (1631-1561 ) استاد هندسه در کالج گرشام در لندن، و بعداٌ استاد در آکسفورد، به ادینبورو سفر کرد تا مراتب احترام خود را به مخترع کبیر لگاریتم‌ها ادا کند. در ضمن این ملاقات بود که نپر و بریگز به این توافق رسیدند که جداول در صورت چنان تبدیلی که لگاریتم 1 ، 0 و لگاریتم 10 هر توان مناسبی از 10 شود، مفیدتر خواهد بود. بدین ترتیب لگاریتم امروزی بریگزی، یا متعارفی، تکوین یافت. این گونه از لگاریتم‌ها، که اساسا لگاریتم‌هایی در مبنای 10 می‌باشند، کارآیی برتر خود را در محاسبات عددی مرهون این حقیقت هستند که دستگاه شمار ما نیز در مبنای 10 است. برای دستگاه شماری که پایه دیگری مانند b داشته باشد، به منظور محاسبات عددی، مناسبتر خواهد بود که جداول لگاریتم نیز در مبنای b باشند.

کلمه لگاریتم به معنی «عدد نسبت» است و توسط نپر، بعد از آنکه از اصطلاح عدد ساختگی استفاده کرد، اتخاذ گردید.

بریگز کلمه مانتیس را، که کلمه لاتینی متاخری از ریشه اتروسکی است، معمول کرد، که در اصل به معنی «جمع» یا «پارسنگ» بوده و در قرن 16 معنی «ضمیمه» را یافت. اصطلاح مفسر توسط بریگر نیز پیشنهاد شد و به وسیله ولاک به کار رفت.

اختراع شگفت انگیز نپر در سرتاسر اروپا به گرمی مورد استقبال واقع شد. در نجوم، بویژه، زمان برای چنان اکتشافی بسیار آماده بود. بنا به اظهار لاپلاس، اختراع لگاریتم ها «با کوتاه کردن زحمات، عمر منجمین را دو  برابر کرد.»

تنها رقیب نپر در پیش قدمی در اختراع لگاریتم بورگی (1632 – 1552 ) ابزار ساز سوئیسی بود. بورگی جدولی از لگاریتم‌ها را مستقل از نپر به تصور در آورده و آنرا ساخت و نتایج کارهای خود را در 1620 شش سال بعد از اینکه نپر کشف خود را به جهانیان اعلام کرده بود، منتشر نمود. گرچه هر دوی آنها ایده لگاریتم را مدتها قبل از انتشار در ذهن خود پروانده بودند، عموما اعتقاد بر این است که این ایده اول بار به ذهن نپر راه یافته بوده است. روش نپر هندسی بود، در حالی که روش بورگی جبری بود. امروزه لگاریتم عموما به عنوان یک نما تلقی می شود.

میله‌های نپر

مشکلی که در ضرب اعداد بزرگ به طور گسترده پیش می‌آمد، منجر به پیدایش طریقه‌های مکانیکی برای انجام این فرآیند گردید. اختراع نپر، مشهور به میله‌های نپر یا استخوان‌های نپر در زمان خود بسیار معروف بود، و توسط کاشف آن در اثری به نام مطالعه چوب‌های معجزه آسا، منتشره در 1617 تشریح شد. این اختراع اصولا همان روش شبکه، یا مشبکه اعراب است.

مثال: ضرب 1615 در 365 ؟
این فرآیند به کمک نوارهای مستطیلی استخوانی، فلزی، چوبی یا مقوایی، که از قبل آماده شده انجام می‌شود. برای هر یک از ارقام دهگانه باید نوارهایی برای عدد 6 نشان داده شده، در اختیار داشت که مضارب مختلف آن رقم را برخود داشته باشد. (یعنی در مربع اول عدد 6 را نوشته سپس در مربعات پایین‌تر مضارب عدد 6 که 12 و 18 و 24 و ... هستند قرار می‌گیرند برای تمام اعداد یک رقمی می توان به این طریق میله‌های موسوم به میله‌های نپری درست کرد)
حال نوارهایی را که در صدر آنها اعداد 1و6و1و5 نوشته شده‌اند، کنار هم قرار می‌دهیم. نتایج ضرب 1615 در ارقام 5و6و3 از عدد 365 را در این صورت می‌توان به آسانی به صورت  8075 و9690 و 4845 پیدا کرد، تنها چند عمل جمع قطری ساده  دو رقم برای به دست آوردن این نتایج لازم اند.

عدد نپر

پرکاربردترین عدد گنگی که بشر تا بحال کشف کرده عدد نپر ( 2.7182 = e)  است. البته اهمیت این عدد بیشتر مرهون کارهای لئونارد اویلر (Leonhard Euler)  دانشمند سوییسی است.چه بسیاری نیز معتقدند انتخاب حرف e  برای عدد نپر بخاطر اولین حرف از نام خانوادگی اویلر بوده است.البته عده‌ای نیز می‌گویند این حرف نخستین حرف کلمه نمایی (exponential) است.

در واقع توابع نمایی بصورت f(x)=a^x  هستند و در بین تمام اعداد حقیقی ممکنی که می‌توانند بجای a  قرار گیرند. عدد نپر تنها عددییست که باعث می‌شود تابع نمایی در نقطه صفر دقیقا شیبی برابر با یک داشته باشد (مشتق تابع e^x  برابر است با e^x  و لذا شیب این تابع در صفر برابر است با e^0=1).

عدد نپر در جاهای دیگر هم ظاهر می‌شود. مثلا فرض کنید در بانک مبلغ یک دلار قرار داده‌اید و بانک به شما 100درصد سود در سال پرداخت می‌کند یعنی در پایان سال شما دو دلار خواهید داشت (n=1) حال اگر بانک بجای صد در صد در سال شش ماه اول 50 درصد سود پرداخت کند (یک و نیم دلار در پایان شش ماه) و در شش ماه دوم نیز 50 درصد سود پرداخت کند (به ازای یک و نیم دلار پس انداز شما) در پایان سال 1.5+0.75=2.25 دلار خواهید داشت (n=2) اگر این بار بانک هر سه ماه یک بار به شما 25 درصد سود پرداخت کند در پایان سال مبلغ 1.25+0.3125+0.390625+0.488281=2.44141 در حساب خود خواهید داشت (n=4) اگر این روند ادامه پیدا کند یعنی بانک در تعداد دفعات بیشتری به شما سود کمتری پرداخت کند و این تعداد دفعات یعنی  n به بینهایت میل کند شما در پایان سال به اندازه  2.7182 = e  دلار در بانک خواهید داشت!!! همچنین اگر احتمال برنده شدن شما در یک بازی n^ -1 باشد و شما این بازی را n  بار انجام دهید و n  به سمت بینهایت میل کند احتمال اینکه شما هر n بازی را ببازید برابر است با  e^ -1

 مرگ

جان نپر سرانجام سه سال پس از انتشار لگاریتم، در چهارم آوریل 1617م در شصت و هفت سالگی درگذشت. یکی از حفره‌های ماه به نام نپر نامگذاری شده‌ است.

گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir