گام به گام ریاضی نهم - فصل 8 - حجم و مساحت
.
.
.
قصل ۸ کتاب ریاضی پایه نهم: در کتاب ریاضی هفتم در مورد شکلهای فضایی، توضیحاتی داشتیم و تقسیمبندی کلی آنها به سه دسته حجم های منشوری، حجم های کروی و حجم های هرمی را انجام دادیم. همچنین در آنجا با دستورات محاسبه مساحت جانبی و کل و حجم منشور و حجم های منشوری آشنا شدیم. در این کتاب دنباله این کار را با ارائه مفاهیم و دستورات مرتبط با حجم های کروی و هرمی پی میگیریم. ابتدا دستور حجم کره را به روش تجربی به دست می آوریم، سپس به دستور مساحت رویه کره با همان روش می پردازیم. در درس دوم دستور حجم هرم را به روشی نسبتاً دقیق به دست می آوریم و کمی هم به مساحت آن توجه میکنیم و دستور حجم مخروط را نیز از تعمیم آن به دست می ّ آوریم و در درس سوم (درس آخر) جمع بندی از دستورات قبلی محاسبه ّ سطح و حجم داریم و در کنار آن نگاهی به تقویت قوهٔ شهود فضایی دانش آموزان نیز داریم. برای این منظور تمریناتی در ارتباط با ایجاد شکلهای فضایی از طریق دوران شکل های مسطح هندسی و نیز کار با گستردهٔ شکل های فضایی و نیز تصور هندسی نسبت به برشهای مقطعی شکل های فضایی داریم.
تصویر عنوانی
یکی از کاربردهای اصلی هندسه، در معماری بناها بوده است و در تاریخ کشورمان از دوران کهن تا معاصر صدها نمونه ممتاز از تأثیر آشنایی دانشمندان، ریاضیدانان و مهندسان و معماران ایرانی با دانش هندسه به وضوح دیده می شود. بنای تاریخی گنبد قابوس واقع در شهر گنبد کاووس که در قرن چهارم هجری بنا شده است یک نمونه از این بناها است. در این بنا حجم های هندسی مانند استوانه، مخروط و منشور به چشم می خورند. تقارن و زیبایی اثر، نمایانگر تسلط کامل معماران آن با دانش هندسه فضایی می باشد.
فصل 8 کتاب ریاضی نهم شامل سه درس می باشد:
- درس اول : حجم و مساحت کره
- درس دوم : حجم هرم و مخروط
- درس سوم : سطح و حجم
حجم و مساحت کره
ابتدای درس، پس از یادآوری انواع حجم ها از کتاب هفتم، تعریف کره با استفاده از مشابهت بین مفاهیم دایره (در صفحه) و کره در فضا انجام می گیرد:
کره مجموعه نقاطی از فضا است که همه آن نقطه ها از یک نقطه در فضا به نام مرکز، به یک فاصله ثابت و مشخص هستند. به این اندازه، شعاع کره میگوییم.
در ادامه با انجام دو فعالیت در صفحات ۱۳۱ و ۱۳۳، دانش آموزان با دستورات محاسبه حجم و سطح کره به طور عملی آشنا میشوند، بدون اینکه نیازی به حفظ کردن آنها داشته باشند. هدف از انجام این دو فعالیت این است که دانش آموزان با این دو اصل آشنا شوند:
- 1- حجم کره ای به شعاع R، برابر ۲/۳ حجم استوانه ای است که این کره در آن قابل محاط شدن است.
- 2- مساحت رویه کره ای به شعاع R، چهار برابر مساحت دایره ای به همین شعاع است.
در کار در کلاس صفحه 132 نیز روی همین موضوع کار شده است و محاسبه ای عملی در ارتباط با حجم کره ای محاط در استوانه انجام میگیرد تا همان فعالیت دوباره به صورت محاسباتی تکرار شود.
در پایان این درس از کتاب ریاضی نهم در صفحه ۱۳۴، سه سوال مهم و نکته دار آورده شده است. در تمرین ۱، هدف کارکردن برروی اعداد بزرگ و یادآوری نماد علمی است. در تمرین ۲، توجه می کنیم که ارتفاع کپسول با ارتفاع استوانه برابر نیست (بدفهمی رایج) ارتفاع نیمکرهٔ بالایی، مساوی شعاع قاعدهٔ استوانه، یعنی 30 سانتیمتر است و لذا ارتفاع استوانه 70 سانتیمتر است.
حجم هرم و مخروط
در ابتدای این درس از کتاب درسی پایه نهم، تعریف های اولیه مربوط به هرم انجام میگیرد. نکته ای که باید به آن توجه کرد و ابهام دانش آموزان را نسبت به آن رفع نمود، این است که قاعده هرم نیز جزء وجه های آن است و در فعالیت صفحه ۱۳۵ درس نیز روی این امر تأکید شده است. در قسمت دوم فعالیت (صفحه 135 و 136) هدف این است که دانش آموزان به طور شهودی به این حقیقت واقف شوند که اگر دو هرم دارای مساحتهای قاعده یکسان و ارتفاع های برابر باشند، حجم های برابر دارند. اثبات دقیق این موضوع به کمک اصل کاوالیری انجام می شود. کار در کلاس صفحه 136 هم معطوف به همین موضوع است. در فعالیت صفحه 137 میخواهیم از همین موضوع استفاده کرده و دستور حجم هرم را استنتاج نمائیم.
کار در کلاس و فعالیت بعدی نیز به کار با دستور حجم هرم اختصاص دارد. در فعالیت صفحه ۱۳۸ کتاب ریاضی، کاربرد قضیه فیثاغورس را در محاسبه ارتفاع هرم منتظم با قاعده مربع می بینیم و از آنجا می توانیم حجم هرم را به دست آوریم. در کار در کلاس صفحه 139، که یادآوری از فعالیتی از کتاب ریاضی هشتم می باشد، مخروطی را به کمک قطاع می سازیم.
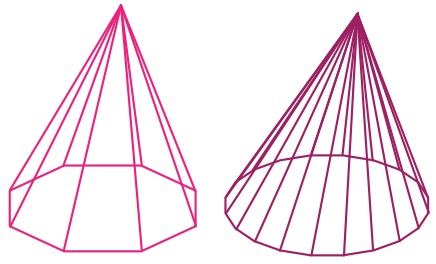
مخروط، شکلی شبیه به هرم منتظم است که قاعده آن به شکل دایره و پای ارتفاع مخروط مرکز این دایره است.
در آخر درس سه سوال به عنوان تمرین در صفحه ۱۳۹ برای تثبیت نکان کلیدی درس آورده شده است.
سطح و حجم
در ابتدای این بخش، فعالیتی (صفحه ۱۴۰) مطرح شده که بی مقدمه، گسترده شکلهای فضایی را مطرح کرده و اندازه ها را روی آن مشخص می کند. دانش آموزان باید بتوانند با توجه به اندازه های روی شکل فضایی آن اندازه ها را در گستردهٔ آن شکل، همانندسازی کرده و از روی آنها مساحتها را اندازه گیری کنند. یکی از محاسباتی که در اینجا یادآوری می شود، استفاده از قضیه فیثاغورس برای محاسبه مساحت مثلثهای متساوی الساقین با استفاده از طولهای ساق و قاعده آنها است.
بخش (2) کار در کلاس هم همین بحث را پی می گیرد (محاسبه مساحت جانبی هرمی با قاعده شش ضلعی منتظم، که مساوی شش برابر مساحت مثلثی متساوی الساقین است.) فعالیت صفحه 141، به هدف سوم، یعنی دوران شکل های هندسی و رابطه آن با شکل های فضایی میپردازد. دانش آموزان باید به این توانایی برسند که بتوانند دوران یافته شکلهای مسطح را در فضا تجسم کرده و آنها را رسم کنند.
به نمونه های زیر توجه شود:
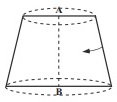 دوران یافتۀ ذوزنقۀ متساوی الساقین حول محور تقارن AB (مخروط ناقص)
دوران یافتۀ ذوزنقۀ متساوی الساقین حول محور تقارن AB (مخروط ناقص)
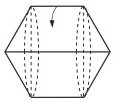 دوران یافتۀ ذوزنقۀ متساوی الساقین حول قاعدۀ بزرگ آن (یک استوانه و دو مخروط متصل به آن)
دوران یافتۀ ذوزنقۀ متساوی الساقین حول قاعدۀ بزرگ آن (یک استوانه و دو مخروط متصل به آن)
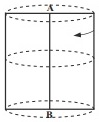 دوران یافتۀ مستطیل حول ضلع AB (استوانه)
دوران یافتۀ مستطیل حول ضلع AB (استوانه)
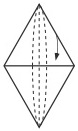 دوران یافتۀ مثلث متساوی الاضلاع حول یک ضلع آن (دو مخروط که قاعدۀ مشترک دارند)
دوران یافتۀ مثلث متساوی الاضلاع حول یک ضلع آن (دو مخروط که قاعدۀ مشترک دارند)
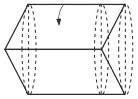 دوران یافتۀ متوازی الاضلاع حول ضلع بزرگ آن (یک استوانه که از یک طرف یک مخروط از آن حذف شده و از طرف دیگر مخروط به آن وصل شده است)
دوران یافتۀ متوازی الاضلاع حول ضلع بزرگ آن (یک استوانه که از یک طرف یک مخروط از آن حذف شده و از طرف دیگر مخروط به آن وصل شده است)
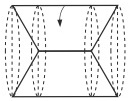 دوران یافتۀ ذوزنقۀ متساوی الساقین حول قاعدۀ کوچک (استوانه ای که دو مخروط از آن حذف شده اند)
دوران یافتۀ ذوزنقۀ متساوی الساقین حول قاعدۀ کوچک (استوانه ای که دو مخروط از آن حذف شده اند)
در کار درکلاس صفحه 142، دانش آموزان می توانند با تجربه قبلی خود، تشخیص دهند که از دوران ربع دایره، حول شعاع آن، یک نیمکره ایجاد می شود و با داشتن طول شعاع آن، حجم آن را به دست آورند. در فعالیت بعدی (در سه قسمت) تمرکز بر روی تقویت حس شهود و تجسم فضایی دانش آموزان است. در قسمت اول و دوم، تجسم نگاه فضایی به یک شکل و تصویری که در ذهن از آن (از سمت و سوهای مختلف) ایجاد می ّ شود مد نظر است. در قسمت سوم و چهارم تمرکز بر روی تقویت حس شهود و تجسم نسبت به مقطع های حاصل از برش شکل های فضایی است. کار در کلاس صفحه 142 نیز همین موضوع را دنبال می کند.
در پایان فصل هشتم کتاب ریاضی پایه نهم، در صفحه ۱۴۳ دو سوال به عنوان تمرین داده شده است. در تمرین ١ نسبت حجم به سطح در مورد چهار شکل خواسته شده است و چنانچه دیده می شود در مورد کره، این نسبت از همه موارد دیگر، بزرگتر است. این نسبت بیانگر آن است که به لحاظ اقتصادی، ساختن شکلها به شکل کره به صرفه تر است، یعنی در میان اشکال هندسی با مساحت برابر، حجم کره بیشتر است، زیرا توزیع حجم آن در سطح واحد، بیشتر است. هدف از تمرین ۲، ایجاد یک شهود ابتدایی نسبت به شکلی فضایی است که از یک ورقه مسطح ساخته می شود.
.
.
.
آموزش مرتبط : فیلم آموزشی تدریس ریاضی نهم - فصل هشتم (کلیک کنید...)
توجه: دانش آموزان عزیز توجه داشته باشید که برای یادگیری بهتر و موفق شدن در امتحان ریاضی پایه نهم بهتر است خودتان روی تمرینات و سوالات خوب فکر کنید و سعی کنید جوابی برای آنها پیدا کنید و در مرحله آخر سراغ جواب بروید. سریعا پاسخ را نگاه نکنید. ابتدا خودتان جوابی بنویسید و بعد راه حل درست را نگاه کنید.
.
.
.
دانلود رایگان راهنمای حل المسائل ریاضی نهم فصل 8
(پسورد فایل Donyaha.ir : PDF)
پاسخنامه مسایل، شرح و توضیحات کلیه نکات کلیدی،جزوه آموزشی، پرسش، دوره متوسطه به صورت تکمیلی کامل پی دی اف منتشران pdf
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
![]()