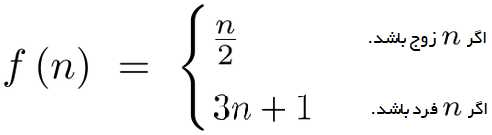معمای مورد بحث «حدس کولاتز» نام دارد. این معما که یکی از گزارههای اثبات نشده در علم ریاضی است، برای اولین بار در سال ۱۹۳۷ توسط ریاضیدان آلمانی، «لوتار کولاتز» مطرح گردید. حدس کولاتز تقریباً برای هر دانشآموزی قابل فهم است. این معما علیرغم ظاهر سادهای که دارد، پس از گذشت ۸۷ سال (تا سال ۲۰۲۴ میلادی) هنوز حل نشده است.
این حدس همچنین به عنوان حدس ۳n+۱ نیز شناخته میشود. این حدس بیان می کند که، صرف نظر از این که چه عددی را به عنوان عدد اولیه انتخاب میکنیم، همیشه به یک صورت تمام میشود.
این حدس تنها از دو قانون اصلی تشکیل شده است:
- قانون اول: در صورتی که n یک عدد طبیعی زوج باشد، باید آن را بر ۲ تقسیم کنیم.
- قانون دوم: اعداد طبیعی فرد باید ابتدا در ۳ ضرب شوند و سپس با عدد ۱ جمع شوند.
یعنی:
مثال: میخواهیم عدد 10 را با حدس کولاتز امتحان کنیم.
10→5→16→8→4→2→1
درستی حدس بالا به وسیلهی کامپیوترهای قدرتمند، تا عدد 2 به توان 60 نشان داده شده است. در عین حال چون اثبات منطقیای وجود ندارد، هنوز ممکن است عددی یافت شود که این حدس را نقض کند.
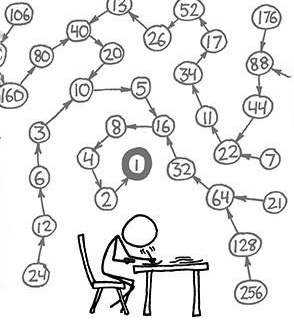
به عنوان یک نتیجهگیری میتوان گفت که اگر روند کولاتز رو معکوس کنیم. باید بتوان تمام اعداد طبیعی را ساخت. البته روند معکوس کولاتز به یک زنجیره خاص منحصر نیست و میتواند چند شاخه شود! مثل عدد 10 در شکل بالا، که اگر معکوس روند کولاتز را دنبال کنیم به دو عدد 3 و 20 میرسیم.
در حین بررسی دنباله کولاتز ممکن است به اعدادی به مراتب بزرگتر از عدد اولیه هم برسیم. ولی بعد از چند تکرار این اعداد دوباره کوچک میشوند تا به عدد یک برسیم. در شکل زیر روند تغییر اعداد دنبالهی کولاتز به ازای اینکه اولین عدد 27 باشد، دیده میشود. محور افقی برابر تعداد تکرار و محور عمودی مقدار عدد دنباله را نشان میدهد. این سری عددی 111 عدد دارد و در بعضی مواقع مقدارش به 9000 نیز میرسد.
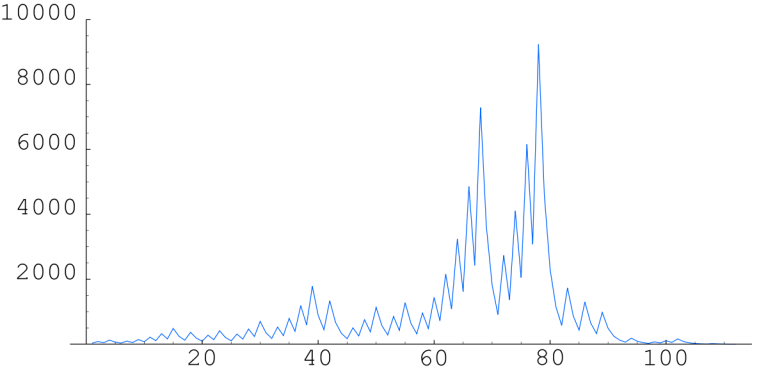
۲۷→ ۸۲→ ۴۱→ ۱۲۴→ ۶۲→ ۳۱→ ۹۴→ ۴۷→ ۱۴۲→ ۷۱→ ۲۱۴→ ۱۰۷→ ۳۲۲→ ۱۶۱→ ۴۸۴→ ۲۴۲→ ۱۲۱→ ۳۶۴→ ۱۸۲→ ۹۱→ ۲۷۴→ ۱۳۷→ ۴۱۲→ ۲۰۶→ ۱۰۳→ ۳۱۰→ ۱۵۵→ ۴۶۶→ ۲۳۳→ ۷۰۰→ ۳۵۰→ ۱۷۵→ ۵۲۶→ ۲۶۳→ ۷۹۰→ ۳۹۵→ ۱۱۸۶→ ۵۹۳→ ۱۷۸۰→ ۸۹۰→ ۴۴۵→ ۱۳۳۶→ ۶۶۸→ ۳۳۴→ ۱۶۷→ ۵۰۲→ ۲۵۱→ ۷۵۴→ ۳۷۷→ ۱۱۳۲→ ۵۶۶→ ۲۸۳→ ۸۵۰→ ۴۲۵→ ۱۲۷۶→ ۶۳۸→ ۳۱۹→ ۹۵۸→ ۴۷۹→ ۱۴۳۸→ ۷۱۹→ ۲۱۵۸→ ۱۰۷۹→ ۳۲۳۸→ ۱۶۱۹→ ۴۸۵۸→ ۲۴۲۹→ ۷۲۸۸→ ۳۶۴۴→ ۱۸۲۲→ ۹۱۱→ ۲۷۳۴→ ۱۳۶۷→ ۴۱۰۲→ ۲۰۵۱→ ۶۱۵۴→ ۳۰۷۷→ ۹۲۳۲→ ۴۶۱۶→ ۲۳۰۸ ۱۱۵۴→ ۵۷۷→ ۱۷۳۲→ ۸۶۶→ ۴۳۳→ ۱۳۰۰→ ۶۵۰→ ۳۲۵→ ۹۷۶→ ۴۸۸→ ۲۴۴→ ۱۲۲→ ۶۱→ ۱۸۴→ ۹۲→ ۴۶→ ۲۳→ ۷۰→ ۳۵→ ۱۰۶→ ۵۳→ ۱۶۰→ ۸۰→ ۴۰→ ۲۰→ ۱۰→ ۵→ ۱۶→ ۸→ ۴→ ۲→ ۱
کوچکترین i که به ازای آن روند فوق ادامه مییابد زمان کلی ایست n نام دارد. این حدس ادعا دارد که هر عدد n یک زمان کلی ایست خوش تعریف دارد. اگر به ازای یک N خاص، عدد i به صورت بیان شده وجود نداشته باشد میگوییم N یک زمان کلی ایست نامحدود دارد و حدس غلط است. اگر حدس غلط باشد میتواند فقط به این دلیل باشد که یک عدد شروعی وجود دارد که به دنباله خاتمهای میدهد که ۱ شامل آن دنباله نیست. یک چنین دنبالهای ممکن است وارد چرخهای شود که از ۱ مستثنی باشد یا این که بدون محدودیت ادامه یابد. تا به حال چنین دنبالهای پیدا نشدهاست.
اثبات استدلال
هرچند که این حدس هنوز اثبات نشدهاست، ولی اکثر ریاضیدانان که این مشکل را بررسی کردهاند، خود به خود اعتقاد دارند که این حدس درست است. در این قسمت دو دلیل برای این انتظار درستی بیان میکنیم:
مدارک آزمایشی
این حدس توسط رایانه برای تمام صحیح مثبت تا ۱۰ × ۲۵۸ ≈ ۲٫۸۸×۱۰۱۸ امتحان شدهاست.
با تعجب باید گفته شود که این گونه مقید کردنها توسط رایانه ارزش مدرکی بسیار محدودی دارند. چندین حدس وجود دارند که مثال نقضشان بهطور استثنایی مقداری بسیار بزرگ است.(مانند حدس پولیا، حدس مرتن یا عدد اسکیوویز) همچنین این موضوع که، {۴٬۲٬۱} تنها چرخه با دورهٔ کمتر از ۳۵۴۰۰ است، روشن شدهاست.
مدارک احتمالی
اگر کسی تنها اعداد فرد تولید شده در دنباله کولاتز را در نظر بگیرد، آنگاه کسی میتواند استدلال کند که در حالت میانگین (در حالت خاص میانگین هندسی قسمتها) عدد فرد بعدی باید ¾قبلی باشد، که اظهار میکند این دسته اعداد باید با ترتیبی طولانی کاهش یابند. (اگرچه این مدرکی علیه چرخهها نیست، فقط علیه واگرایی است)
حل مسئله
تاکنون خبر جدیدی در مورد حل این معما مطرح نشده بود. به تازگی، ترنس تائو پست جدیدی را در وبلاگ شخصی خود منتشر کرده، که به حدس کولاتز ارتباط دارد. او در این پست گفته که «تقریباً همهی مدارهای کولاتز به مقادیر نسبتاً جفتشده منتهی میشوند».
حال، ابتدا باید با مفهوم «مدار کولاتز» آشنا شویم، که اتفاقاً بسیار ساده است. مدار کولاتز به توالیهای خاصی اطلاق میگردد، که از هر عدد طبیعی خاص در این معادله حاصل میشود. برای مثال، مدار کولاتز عدد ۱۰ عبارت است از:
۱۰, ۵, ۱۶, ۸, ۴, ۲, ۱, ۴, ۲, ۱, …
بنابراین، مدار کولاتز از همهی عددهایی تشکیل میشود، که به عنوان جواب برای یک عدد طبیعی خاص به دست میآیند. از آنجایی که پاسخ نهایی برابر با یک است، مقدار معادلهی دوم (۳n + 1) برابر با ۴ خواهد بود. این چهار نیز بر اساس معادله به ۲ خواهد رسید. بنابراین، تمام مدارهای کولاتز به توالی (۱، ۲، ۴) ختم خواهند شد. این توالی سهتایی تا ابد در داخل حدس کولاتز ادامه پیدا خواهد کرد. این از مفهوم مدار کولاتز.
نکتهی مهم دیگر در مورد ادعای ترنس تائو، الفاظ «تقریباً» و «نسبتاً» است. «تقریباً» معمولاً حکم آخرین مانع در رسیدن به جواب یک معادله را دارد. این لفظ در زمینههای گوناگون ممکن است معانی متفاوتی داشته باشد. اما منظور تائو از «تقریباً» چه بوده است؟
«تقریباً» در این بیان به مفهوم «تراکم لگاریتمی» است. به عبارت دیگر، منظور تائو این است که احتمال پیدا کردن عددی که بتواند جواب نهایی حدس کولاتز را نقض کند، بسیار کم است. چنین عدد یا عددهایی ممکن است وجود داشته باشد، اما با پیشروی در مسیر اعداد طبیعی، فراوانی چنین عددی به صفر میل میکند. هدف تائو اثبات این قضیه است که چنین عددی عملاً وجود ندارد.
مطابق با فرضیهی تائو، احتمال کشف مثال ناقض برای حدس کولاتز بینهایت کم است. باید توجه کرد که حتی «بینهایت کم» با «صفر» تفاوت دارد، و همچنان احتمال وجود داشتن چنین عددی فراهم است.
خب، اکنون که احتمال وجود مثال ناقض در این معادله به حداقل میزان خود رسیده، آیا حدس کولاتز را باید حل شده به حساب بیاوریم؟
پاسخ کاملاً مثبت نیست. ولی میتوان ادعا کرد که تا چند دههی آینده، حدس کولاتز همچنان یک حدس باقی خواهد ماند. چون ما هنوز نتوانستهایم احتمال وجود مثال ناقض را برای آن کاملاً رد کنیم.
نامهای دیگر
همچنین این مسئله را به نامهای زیر نیز میشناسند:
- مسئله 3n+۱
- حدس 3n+۱
- حدس اولام (به یاد استنیسواف اولام)
- مسئله کاکوتانی (به یاد شیزو کاکوتانی)
- حدس توایتس (به یاد برایان توایتس)
- الگوریتم هاسه (به یاد هلموت هاسه) یا مسئله سیراکوس
دنباله اعداد ظاهر شده در این حدس را برخی مواقع دنباله تگرگی یا اعداد تگرگی (به این دلیل که مقادیرش اغلب همچون تگرگ درون یک ابر، چندین نزول و صعود دارند) یا اعداد شگرف مینامند.
پاول اردوش در مورد حدس کولاتز گفت:
«ممکن است ریاضیات برای چنین مسائلی هنوز آمادگی نداشته باشد.»
همچنین او جایزه ۵۰۰ دلاری را برای جواب آن اعلام نمود. جفری لاگاریاس در ۲۰۱۰ بیان نمود که حدس کولاتز «مسئلهای است که دشواری عجیباً زیادی داشته و کاملاً از دسترس ریاضیات کنونی خارج است.»
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
![]()