آرتور کیلی، ریاضیدانی بریتانیایی بود که بیشتر روی جبر کار می کرد و او به پیدایش مکتب ریاضی محض مدرن کمک بسیاری کرد. او به تأسیس مدرسه بریتانیایی ریاضیات محض کمک کرد و به مدت 35 سال در کالج ترینیتی کمبریج استاد بود.
بزرگترین کار او، که با همکاری جیمز جوزف سیلوستر انجام شد، ابداع نظریه ناوردا ها بود (این نظریه نقش مهمی در نظریه نسبیت ایفا کرد). کیلی، سهم بسزایی در هندسه n بعدی دارد و نظریه ماتریسها را نیز ابداع کرد.
زندگی
آرتور کیلی در سال 1821 در ریچموند متولد شد و در سال 1838 وارد کالج ترینیتی در کمبریج شد و تنها قبل از فارغالتحصیلی 3 مقاله به چاپ رساند. او تحصیلات خود را در رشته حقوق ادامه داد، ولی پس از 14 سال دوباره به عالم ریاضیات بازگشت.
کیلی سومین نویسنده کثیرالتالیف ریاضیات در تاریخ این موضوع است، و تنها اویلر و کوشی بر او پیشی دارند. وی موقعی که هنوز دانشجوی دوره لیسانس در دانشگاه کمبریج بود، به نشر آثار پرداخت و طی عمر طولانیش به کار نشر پرکثرت خود ادامه داد.
در دوبلین با چهارگانهای (Quaternions) همیلتون آشنا شد و از آن پس ریاضیات را به طور جدی ادامه داد. او موجب پیشرفت زیادی در نظریه ماتریسها شد و تحقیقات بسیاری در هندسه نااقلیدسی ، نظریه گروهها و گروههای جایگشتی انجام داد.
مقالات و آثار کیلی
"مجموعه مقالات ریاضی" حجیم کیلی مشتمل بر 966 مقاله است و 13 مجلد بزرگ به قطع ربعی به طور متوسط 600 صفحه در هر جلد را پر میکند. به ندرت میتوان زمینهای در ریاضیات مجرد را سراغ گرفت که نبوغ کیلی بر آن دست نیازیده باشد یا بر غنای آن نیفزوده باشد.

مبتکر نظریه ماتریسها آرتور کیلی است. وی سهم پیشتازانه ای در هنسه تحلیلی، نظریه تبدیلها، نظریه دترمینانها، هندسه با ابعاد بالاتر، نظریه افراز، نظریه منحنیها و رویهها، مطالعه صورتهای دودویی و سه سه یی، نظریه تابعهای آبلی، تتا و بیضوی دارد.
مقالههای کیلی دقیق، سر راست، با اسلوب و روشناند.
وی حافظهای شگفت انگیز داشت و چنین مینمود که هرگز چیزی را که دیده یا خوانده، فراموش نمیکند. وی همچنین خویی به طور استثنایی آرام و ملایم داشت. او را «ریاضیدان ریاضیدانان» نامیدهاند.
آرتور کیلی تقریبا بر همه شاخههای ریاض عصر خود مسلط بود و به همین خاطر از استثناهای دنیای ریاضیات محسوب میشود . از مجموع مقالات وی حدود 250 مقاله مربوط به دوران حقوقدانیاش میباشد.
قضیه کیلی-همیلتون
در جبر خطی و نظریه ماتریسها، قضیه کیلی - همیلتون که به نام آرتور کیلی و ویلیام روان همیلتون نامگذاری شده است بیان میکند که هر ماتریس مربعی (بر روی یک حلقه جابهجایی مثل میدان اعداد حقیقی یا میدان اعداد مختلط) در معادله مشخصه خود صدق میکند.
گراف کیلی
در ریاضیات یک گراف کیلی، گرافی است که ساختار جبری یک گروه جبری را در خود دارد. نام گراف کیلی پس از قضیهٔ کیلی پیشنهاد شد که در تعریف آن یک گروه به همراه مجموعهای از عناصر آن (معمولاً مولد آن گروه) در نظر گرفته میشود.
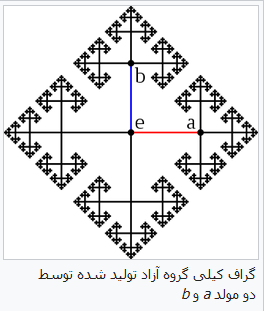
G یک گروه، و S یک مجموعة مولد برای آن باشد. گراف کیلی Γ = Γ ( G , S ) از عناصر گروه به عنوان رئوس گراف تشکیل شدهاست طوری که بین هر کدام از این رئوس (عناصر گروه) یک یال وجود دارد هرگاه عضوی از S وجود داشته باشد که با ضرب در یکی از رئوس دیگری را بسازد. مثلاً برای عضو دلخواه g در G همهٔ عناصری به شکل g ∗ s که s در S تغییر میکند به g متصلاند. پس هر گراف کیلی منظم است. چون هر راس آن از درجهٔ | S | است.
مرگ او
کیلی در سال 1895 درگذشت.
در هر چیز از جمله یک نظریه ریاضی زیبایی را میتوان درک کرد اما نمیتوان توضیح داد...آرتور کیلی
گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
![]()


