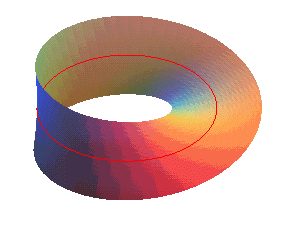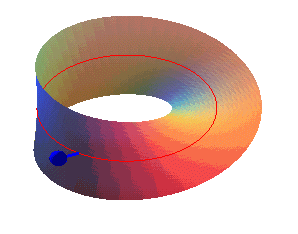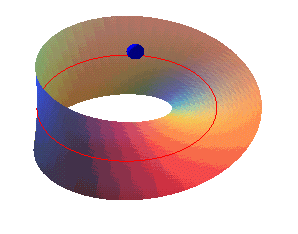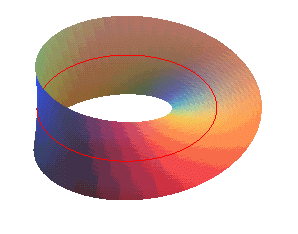نکات جالب درباره نوار موبیوس - بطری کلاین

ریاضیات پر از شگفتی است. این شگفتی‌ها بیشتر حاصل همخوانی نظریات مجرد ریاضی با طبیعت عینی و ملموس پیرامون ماست.

نوار موبیوس یکی از هزاران موضوع جالبی است که هم از لحاظ نظری و هم از لحاظ هندسی جذابیت‌های ویژه‌ای برای ریاضیدانان دارد. برای آشنایی با نحوه ساختن این نوار و ویژگی‌های آن بهتر است آنرا با یک نوار استوانه‌ای مقایسه کنیم. در حالی که یک نوار استوانه‌ای با چسباندن دو سر یک نوار باریک بطور ساده بدست می‌آید، برای ساختن یک نوار موبیوس باید ابتدا یک سر نوار را 180 درجه بچرخانید سپس آنرا به سر دیگر نصب کنید.

این نوار مستقلا و به طور جداگانه توسط دو ریاضیدان آلمانی به نامهای آگوست فردیناند موبیوس  (August Ferdinand Möbius) و جان بندیکت (Johann Benedict) در سال ۱۸۵۸ کشف و به ثبت رسید.

روش ساخت

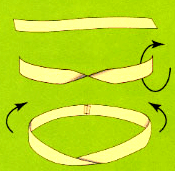
ابتدایی‌ترین راه برای ایجاد این نوار، انتخاب یک نوار مستطیل شکل، دراز و نرمی است که آن را یک بار می‌پیچانیم و سپس دو انتهای آن را به هم متصل می‌کنیم. سطحی که به این ترتیب به دست می‌آید «نوار موبیوس» نامیده می‌شود.

این سطح تنها یک رو دارد. به بیان دیگر، یک صفحه کاغذی را می‌توان با دو رنگ گوناگون در دو طرف آن رنگ کرد اما نوار موبیوس را با این روش نمی‌توان با دو رنگ مختلف رنگ کرد. در صورت اقدام به چنین کاری به همان جایی که رنگ کردن را در ابتدا آغاز کرده‌ بودیم، می‌رسیم؛ در حالی که در طرف دیگر نوار هستیم! پس نوار موبیوس، سطحی است که یک رو دارد و حرکت ما روی آن، تا بینهات بار تکرار می‌شود.

تعریف خاص ریاضی تک رویه بودن

دلیل «یک رویه بودن» این نوار آن است که در هر نقطه a از نوار موبیوس می‌توان دو بردار با جهت‌های مختلف رسم کرد که بر نوار موبیوس در این نقطه عمود باشد.

این بردارها را قائم‌های نوار موبیوس در نقطه a می‌نامیم. یکی از این بردارها را انتخاب و نقطه a را به تدریج روی نوار موبیوس جابجا می‌کنیم. در این صورت بردار ما هم همراه با نقطه a جابجا می‌شود. بنابراین، روی نوار موبیوس چنان مسیر بسته‌ای وجود دارد که اگر قائمی این مسیر را روی سطح بپیماید، به جای این که به وضع نخستین خود برسد، روی برداری که در جهت مخالف وضع نخستین آن است قرار می‌گیرد.

مفهوم مرزِ ناحیه (اثبات تک رویه بودن)

مرز یک ناحیه در فضا: مرزِ یک ناحیه، خط جدا کننده آن ناحیه از ناحیه دیگر است. در ریاضیات برای یک سطح سه مفهوم تعریف می شود:

• ۱- نقطه داخلی: نقطه‌ای که بتوان آن را داخل یک دایره روی سطح محصور کرد.
• ۲- نقطه خارجی: نقطه‌ای است که بتوانیم دایره ای حول آن رسم کنیم که متعلق به آن سطح نباشد.
• ۳- نقطه مرزی: نقطه‌ای است که هر دایره‌ای حول آن رسم شود، قسمتی از آن متعلق به سطح و قسمت دیگر آن متعلق به خارج آن سطح باشد.

با این تعریف نوار موبیوس فقط یک مرز دارد. یعنی با یک بار حرکت در کرانه‌های انتهای نوار تمام مرز آن را می‌توانیم طی کنیم.

کاربرد خواص آن در معماری

خاصیت موبیوسی: خاصیتی است که رابطه بین «درون» و «بیرون» را وارونه می‌کند. یعنی هر نقطه از یک سطح موبیوسی در عین حال که درون است، بیرون نیز می‌باشد! بنابراین در یک تغییر پیوسته، نوعی دگرگونی در ماهیت یک فضا صورت می‌گیرد. در واقع در این حالت فضا خاصیت دوگانه اما پیوسته پیدا می‌کند.

خاصیت موبیوس که گذر از درون به برون و از برون به درون را ممکن می‌کند، کمابیش توانسته است بر فراز شکاف حاصل از دوگانگی (ثنویت) پلی بزند. بنابراین، فضای میان «برون و درون»، «پیوستگی» و «تکرار» با یک تعریف ریاضی به یک سطح هندسی تبدیل می‌شود. سطحی که بر آن در هر لحظه ای هم داخل و هم خارج فضا هستیم. این ویژگی در طراحی معماری مورد توجه قرار گرفته است.

فرشید موسوی در پروژه‌ای به نام خانه مجازی (Virtual House) از خاصیت نوار موبیوس برای طراحی استفاده می‌کند. او با این ساختار، سطح توپولوژیکی به وجود می‌آورد که در آن هر اتاق با اتاق دیگر ترکیب می‌شود تا نواری دو طرفه و دو منظوره را درست کند. در آن پروژه تـضاد بین داخل-خارج، جلو-عقب، پائین-بالا و دیگر مفاهیم در یک سکونتگاه مورد پرسش قرار می‌گیرد و ارتباطی خاص میان این مفاهیم به وجود می‌آید.

ساختار هندسی نوار موبیوس، «درون و بیرون» با «داخل و خارج» را تلفیق می‌کند و فضای سومی با کیفیتی جدید به وجود می‌آورد. این فضای سوم، فضایی است که «همزمانی»، «تبدیل» و «تکرار» در میان پدیده ها در آن رخ می‌دهد.

نکات جالب

اگر با یک خودکار بر روی نوار موبیوس خطی در طول نوار بکشیم و ادامه دهیم این خط دوباره به نقطه شروع باز می‌گردد و هر دو طرف نوار خط کشیده می‌شود! در واقع، نوار موبیوس مثالی از یک رویه بدون جهت (جهت ناپذیر) است. یعنی نوار موبیوس سطحی است که یک رو دارد. از خواص حیرت آور این نوار آن است که این نوار فقط یک مرز دارد.

اشر (Escher) هنرمند معروف این خاصیت را به زیباترین وجهی در نقاشی خود نشان داده است. در این نقاشی یک مورچه دیده می شود که بدون نیاز به عبور از لبه نوار می تواند بطور نامحدود در طول نوار موبیوس حرکت کند.

نوار موبیوس خواص غیرمنتظره دیگری نیز دارد؛ برای نمونه، هرگاه بخواهیم این نوار را در امتداد طولش بِـبُریم به جای این که دو نوار به دست بیاوریم، یک نوار بلندتر و با دو چرخش به دست می آوریم! همچنین با تکرار دوباره این کار دو نوار موبیوس در هم پیچ خورده به دست می‌آید.

با ادامه این کار یعنی بریدن پیاپی نوار، در انتهای کار تصاویر غیرمنتظره‌ای ایجاد می‌شود که به حلقه‌های پارادرومیک (paradromic rings) موسومند. همچنین اگر این نوار را از یک سوم عرض نوار ببریم، دو نوارِ موبیوس در هم گره شده با طول‌های متفاوت به دست خواهیم آورد. تمامی این کارها به آسانی قابل اجرا هستند.

نمونه دیگر موبیوسی: بطری کلاین

فلیکس کلاین، ریاضیدان آلمانی و عضو آکادمی علوم برلین در سال ۱۸۸۲ نمونه جالبی از سطح یک رویه طرح کرد که به «بطری کلاین» معروف شده است. این بطری سطح کاملاً بسته‌ای دارد. با وجود این، برای آن نمی‌توان رویه داخلی یا خارجی معلوم کرد و به عبارتی دیگر حجم آن صفر است. این شکل هم مثل نوار موبیوس داری یک رویه است ولی بر خلاف آن هیچ کناره‌ای ندارد. می‌توان برشی از آن بدست آورد که هر نیمه آن یک نوار موبیوس تشکیل دهد. بطری کلاین را می‌توان به هر طرفی چرخاند بدون اینکه هیچ اتفاقی برای مایع درون آن بیفتد.

نظریات در کیهان شناسی

در کیهان شناسی مطرح شده است که کیهان را به شکل زین اسب می‌داند و اشکالی نیز به نام بطری کلاین و نوار موبیوس ارائه شده است. در بطری کلاین جهان بسته است و به شکل یک بطری است در نوار موبیوس جهان درون و بیرون ندارد، اگر حرکت در جهان را از جایی شروع کنیم که روی نوار باشد که سرانجام از زیر نوار سر درمی آوریم و یا اگر از زیر آن شروع کنیم به روی آن خواهیم آمد.

گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir