جواب کامل تمرینات و حل سوالات کتاب ریاضی هشتم فصل سوم (۳)

گام به گام ریاضی هشتم - فصل 3 - چندضلعی ها

.

.

.

در ابتدای فصل سوم کتاب ریاضی هشتم تصاویری از فرش‌بافی و معماری سنتی، اسلامی ایرانی به نمایش درآمده است؛ که در آنها، انواع نقش‌های هندسی و ترکیب چند ضلعی‌های مختلف در منبت‌کاری، شیشه‌کاری، آینه‌کاری، کاشی‌کاری و سایر صنایع دستی و نقوش معماری دیده می‌شود. طی هزاران سال گذشته، در آثار هنری گوشه و کنار کشور پر افتخارمان، نقش مؤثر استفاده از هندسه و اشکال هندسی و نیز مفاهیم مهم هندسی همچون انتقال، تقارن و دوران به وضوح قابل مشاهده می‌باشد.

این فصل شامل پنج درس، همراه با مرور فصل می‌باشد :

• درس اول : چندضلعی‌ها و تقارن
• درس دوم : توازی و تعامد
• درس سوم : چهارضلعی‌ها
• درس چهارم : زاویه‌های داخلی
• درس پنجم : زاویه‌های خارجی
• مرور فصل ۳

چندضلعی‌ها و تقارن

فعالیت صفحه ۳۰ با تعریف چندضلعی و شرایط آن شروع می‌شود و بیان می‌کند که ؛ در صفحه به هر خطِ شکسته‌ی بسته، چندضلعی گفته می‌شود به شرط آنکه ضلع‌ها یکدیگر را قطع نکنند؛ مگر در رأس‌ها که دو ضلع به هم می‌رسند.

مثلا:

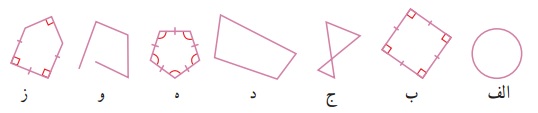
• شکل «الف» چندضلعی نیست؛ چون شکسته نیست.
• شکل «ج» چندضلعی نیست؛ چون ضلع‌های آن یکدیگر را قطع کرده‌اند.
• شکل «و» هم چندضلعی نیست؛ چون بسته نیست.

در ادامه به تعریف چندضلعی منتظم پرداخته شده است و بیان کرده که وقتی؛ در یک چندضلعی همه‌ی ضلع‌ها با هم و همه‌ی زاویه‌ها با هم مساوی باشند، می‌گوییم آن چندضلعی، منتظم است.

مثلا:

• ۳ ضلعی منتظم: مثلث متساوی‌الاضلاع
• ۴ ضلعی منتظم: مربع
• چندضلعی‌های منتظم بالاتر: اسم خاص ندارند.

در ادامه درس اول فصل ۳ کتاب ریاضی هشتم، خط تقارن شکل‌ها (منتظم) یادآوری شده است و فعالیت صفحه ۳۱ و ۳۲ مرکز تقارن را برای دانش‌آموزان توضیح داده است و به این موضوع اشاره می‌کند؛ اگر شکلی را حول یک نقطه، ۱۸۰ درجه دوران دهیم و نتیجه دوران روی خودش منطبق شود، می‌گوییم شکل مرکز تقارن دارد و نقطه مورد نظر، مرکز تقارن شکل است.

توجه مهم :

بعضی شکل‌های منتظم (تعداد اضلاع فرد) می‌توانند چندین خط  تقارن داشته باشد اما شاید مرکز تقارن نداشته باشند.

کار در کلاس و تمرین‌های صفحه ۳۳، به موضوع، مرکز تقارن پرداخته است.

توازی و تعامد

اگر خطی مانند d₁ خطوط a و b را با زاویه‌های مساوی قطع کرده باشد، خط‌های a و b با هم موازیند. به خط d₁ خط مورب می‌گویند. موازی بودن خط‌های a و b را به صورت a||b نمایش می‌دهند. هر خطی که دو خط موازی را قطع کند، با آنها زاویه‌های مساوی می‌سازد. (قضیه خطوط موازی و مورب)

در فعالیت صفحه ۳۴ کتاب درسی ریاضی هشتم، با یادآوری دو زاویه مکمل (مجموع دو زاویه که ۱۸۰ درجه باشند) و زاویه‌های متقابل به راس از دانش‌آموزان می‌خواهد به حل سوالات بپردازند. و کلمات توازی (موازی بودن) و تعامد (عمود بودن) را به آنها یادآوری می‌کند. ( «خط l₁ بر خط l₂ عمود است» را به صورت l₁ ⊥ l₂ می‌نویسیم.)

صفحه ۳۶، شامل ۳ جای خالی بسیار مهم است.

• دو خط عمود بر یک خط، با هم موازیند.
• اگر خطی بر یکی از دو خط موازی عمود شود، بر دیگری نیز عمود است.
• دو خط موازی با یک خط، با هم موازیند.

تمرین صفحه ۳۷، دو سوال مهم و خوب دارد که سعی کنید آنها را به دقت حل کنید.

چهارضلعی‌ها

چهارضلعی‌ای که ضلع‌های روبروی آن دو به دو با هم موازی‌اند، متوازی الاضلاع نام دارد. در اینجا چند چهارضلعی دیگر هم تعریف شده‌اند. (دقت کنید؛ همگی آنها متوازی‌الاضلاع‌اند.)

• مستطیل متوازی‌الاضلاعی است که زاویه‌های قائمه دارد.
• لوزی متوازی‌الاضلاعی است که چهار ضلع آن برابرند.
• مربع متوازی‌الاضلاعی است که چهار ضلع مساوی و زاویه‌های قائمه دارد.

کار در کلاس صفحه ۴۰ ریاضی هشتم سعی دارد به دانش‌آموزان بفهماند که همگی موارد بالا متوازی‌الاضلاع هستند و نکات زیر را می‌توان از شکل سوال ۱ برداشت کرد:

• مربع، نوعی مستطیل است.
• مربع، نوعی لوزی است.
• مستطیل، نوعی مربع نیست.
• لوزی، نوعی مربع نیست.

در تمرینات صفحه ۴۱، هم به بحث موازی بودن ۳ خط و هم اینکه در متوازی‌الاضلاع‌ها، زاویه‌های روبرویشان برابرند؛ پرداخته شده است. سپس در سوال ۴، در مورد ویژگی قطرهای مستطیل و لوزی از دانش‌آموز می‌خواهد، درستی یا نادرستی هر یک از جمله‌های داده شده را بررسی کنند.

زاویه‌های داخلی

زاویه‌هایی که درون یک چندضلعی قرار دارند، زاویه‌های داخلی آن چندضلعی نامیده می‌شوند. مجموع زاویه‌های داخلی یک مثلث ۱۸۰ درجه است و از روی آن، می‌توان به این نتیجه رسید که مجموع زاویه‌های داخلی یک چهارضلعی با مجموع زاویه‌های داخلی دو تا مثلث برابر است؛ پس مجموع زاویه‌های داخلی هر چهارضلعی ° ۳۶۰ می‌شود.

پس برای بدست آوردن مجموع زوایای داخلی چندضلعی‌ها کافی است از تعداد ضلع‌هایشان ۲تا کم کرد؛ عدد بدست آمده می‌شود تعداد مثلث‌های تشکیل شده از یک راس؛ و این عدد را در ۱۸۰، ضرب می‌کنیم.

یعنی :

° ۱۸۰×(۲ - n) = مجموع زاویه‌های داخلی یک n ضلعی

کتاب، در تمرینات صفحه ۴۵ ریاضیات هشتم، با آوردن چند سوال در مورد کاشی و کاشی‌کاری، همچنین تکه‌ای از یک بشقاب قدیمی، سعی کرده که این فصل را با توضیحاتی که در ابتدای فصل آورده بود پیوند بزند و به نوعی کاربرد فصل سوم را در این تمرین آورده است.

زاویه‌های خارجی

زاویه‌ای که در هر رأس یک چند ضلعی محدب، بین یک ضلع و امتداد ضلع دیگر تشکیل می‌شود، زاویه خارجی آن رأس نامیده می‌شود. زاوبه خارجی و داخلی مجاور همدیگر، با هم مکمل‌اند. پس می‌توان ابتدا زاویه داخلی را بدست آورد و از ۱۸۰ کم کرد. اما برای بدست آوردن مجموع زاویه‌های خارجی یک چندضلعی لازم نیست به خودتان زحمت بدهید؛ چون همیشه برابر ° ۳۶۰ است.

نکته: برای بدست آوردن هر یک از زاویه‌های خارجی جندضلعی‌های منتظم کافی است ۳۶۰ را بر تعداد ضلع‌ها (زاویه‌ها) تقسیم کرد.

در سوال ۲ تمرین‌های صفحه ۴۶ کتاب درسی ریاضی هشتم، یک سوال در مورد اثبات اینکه چرا مجموع زاویه‌های خارجی ° ۳۶۰ است و از دانش‌آموزان می‌خواهد؛ با محاسبه زاویه‌های داخلی هر کاشی منتظم، نشان دهند زاویه مشخص شده در هر شکل ۳۶۰ درجه است.

مرور فصل ۳ و تمرین‌های ترکیبی صفحه ۵۰

• بررسی مرکز تقارن یک شکل
• پیدا کردن زاویه‌های مساوی و مکمل در خط‌های موازی و مورب
• تعریف متوازی‌الاضلاع
• تعریف مستطیل
• تعریف لوزی
• تعریف مربع
• خاصیت‌های چهارضلعی‌ها
• پیدا کردن مجموع زاویه‌های داخلی یک چندضلعی
• پیدا کردن زاویه داخلی یک چندضلعی منتظم
• پیدا کردن مجموع زاویه‌های خارجی یک چندضلعی
• پیدا کردن زاویه خارجی یک رأس مثلث

.

.

.

آموزش مرتبط : فیلم‌های آموزشی تدریس ریاضی هشتم - فصل سوم (کلیک کنید ...)

توجه : دانش‌آموزان عزیز توجه داشته باشید که برای یادگیری بهتر و موفق شدن در امتحان ریاضی پایه هشتم بهتر است خودتان روی تمرینات و سوالات خوب فکر کنید و سعی کنید جوابی برای آنها پیدا کنید و در مرحله آخر سراغ جواب بروید. سریعا پاسخ را نگاه نکنید. ابتدا خودتان جوابی بنویسید و بعد راه‌حل درست را نگاه کنید.

.

.

.

دانلود PDF رایگان حل‌المسائل ریاضی هشتم فصل ۳

گردآورنده: دنیاها، دانشنامۀ فارسی | www.Donyaha.ir