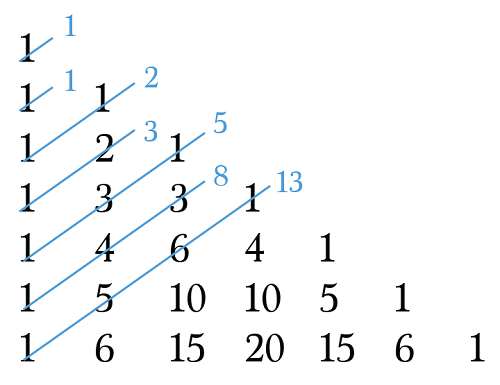
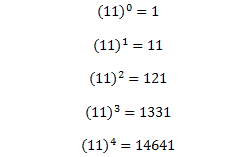مثلث خیام پاسکال یک ساختار عددی است که خواص بسیار جالبی دارد. مثلث خیام-پاسکال به آرایش مثلث شکل ضرایب بسط دوجملهای گویند.
خواص این مثلث را در آسیا و اروپا ریاضیدانان مختلفی بررسی کردهاند. ایران، هند، چین و ایتالیا از جمله این کشورها هستند. به عنوان مثال پینگالا از هند و عمر خیام از ایران در زمان مشابهی اولین استفادهها از این مثلث را در رسالههای خود بکار بردهاند. به عنوان مثال در آثار خواجه نصیر الدین طوسی از مثلث خیام پاسکال برای محاسبهی ضرایب بسط یک عبارت جبری استفاده شده است.
بعد از عمر خیام، در قرن 12 میلادی، در آثار یانگ هویی (ریاضی دان چینی) نیز ساختار عددی مثلث خیام پاسکال دیده شده است.
در قرن 16 تارتالیا (ریاضی دان ایتالیایی) و بعد از او بلز پاسکال و نیوتن نیز بر روی مثلث خیام کار کردهاند. راجع به این که دانشمندان مختلف به صورت مستقل و بدون آگاهی از کارهای قبل از خودشان به کشف این مثلث رسیدهاند یا نه اختلافات تاریخی ممکن است وجود داشته باشد. این موضوع را از روی اسامی مختلف این مثلث میتوان فهمید مثلاً مثلث خیام، مثلث خیام پاسکال، مثلث نیوتن و …. این موارد نشان میدهد که ممکن است به لحاظ تاریخ علم برخی اعتقاد به کشف مستقل این مثلث از سوی دانشمندان مختلف داشته باشند.
نامگذاری و تاریخچه
«مثلث خیام-پاسکال» را «مثلث خیام-پاسکال-نیوتن» نیز میگویند. این مثلث توسط دانشمندان گوناگونی از هند و ایران و چین و غیره و بعدتر در اروپا بررسی شدهاست و در زبانهای گوناگون، نامهای مختلفی دارد. در زبان انگلیسی «مثلث پاسکال»، ایتالیایی «مثلث تارتالیا» و در زبان چینی «مثلث یانگ هویی» نام گرفته است. در آثار متون سانسکریتِ پینگالا ریاضیدان هندی نشانههایی از استفاده از این بسط دیده میشود. در همان دوران عمر خیام ریاضیدان ایرانی ادعای کشف روشی جبری برای به دست آوردن ضرایب بسط دوجملهای میکند.
کتاب مشکلات الحساب، کتابی که اثباتهای این ادعا در آن آمده هنوز کشف نشده ولی در آثار طوسی تأثیر گرفته از او ضرایب را تا توان ۱۲ میتوان دید. بعد از او در قرن ۱۲ میلادی در آثار یانگ هویی ریاضیدان چینی، شکل مثلث به چشم میخورد. در قرن ۱۶ میلادی ریاضیدان ایتالیایی تارتالیا هم از خود این مثلث را به جا گذاشته و پس از یک قرن پاسکال ریاضیدان فرانسوی هم دوره با نیوتن روی این بسط و مثلث حسابی آن کار کرد.
مثلث خیام چیست؟
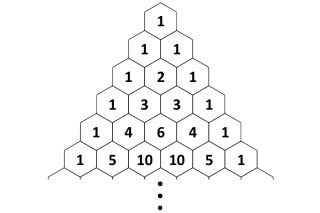
این ساختار عددی در اطراف خود اعداد یک را دارد. هر عدد در این مثلث مجموع دو عددی است که در بالا، و سمت چپ و راست آن قرار دارند. برای مثال:
1 + 1 = 2
1 + 2 = 3
1 + 3 = 4
برای درک بهتر انیمیشن زیر را نگاه کنید:
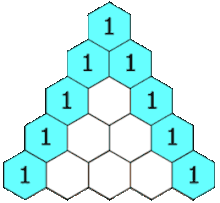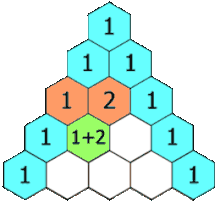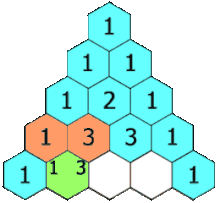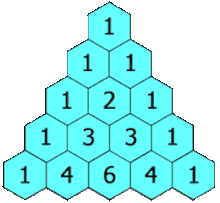
مثلاً عدد 6 میانی حاصل جمع دو عدد 3 بالا سر خود است. یا عدد 5 حاصل جمع 4 و 1 بالاسر خودش است. اگر دقت کنید این یک ساختار متقارن است. یعنی یک خط تقارن مرکزی میتوان برای مثلث بالا رسم کرد. مثلاً در سطر پنجم دو عدد 4 در اطراف عدد مرکزی ( عدد 6 ) به صورت متقارن قرار دارند.
کاربرد و خواص
کاربرد اول:
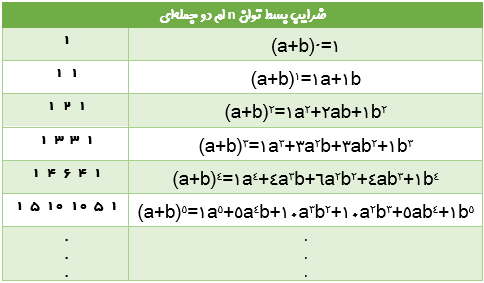
مهمترین کاربرد این مثلث در محاسبه ضرایب بسط دو جملهای نیوتن است. ضرایب بسط توان nام دو جملهای در سطر n+1 قرار دارد.
کاربرد دوم:
اگر به جای a و b عدد یک را بگذاریم چه اتفاقی میافتد؟ خاصیت جالب بعدی این است که مجموع اعداد هر سطر از مثلث، یکی از توانهای عدد 2 است:
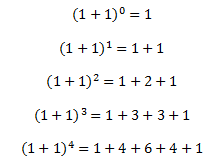 به عبارت دیگر ( 1+1 ) n برابر 2n است که با جمع اعداد سطر n+1ام مثلث خیام پاسکال بدست میآید.
به عبارت دیگر ( 1+1 ) n برابر 2n است که با جمع اعداد سطر n+1ام مثلث خیام پاسکال بدست میآید.
![]() تمرین 1: با استفاده از مثلث خیام پاسکال حاصل 28 رابیابید؟
تمرین 1: با استفاده از مثلث خیام پاسکال حاصل 28 رابیابید؟
پاسخ: برای محاسبه 28 باید اعداد سطر نهم مثلث خیام پاسکال را باهم جمع کنیم.
28 =1+8+28+56+70+56+28+8+1=256
کاربرد سوم:
یک ارتباطی بین توان های مختلف عدد 11 و مثلث خیام پاسکال موجود است. یکی از زیباترین خواص این مثلث آن است که اگر اعداد هر سطر را چسبیده به هم بنویسیم، اعداد حاصل توانهای 11 خواهند بود:
توجه کنید:
همانطور که مشاهده میکنید برای محاسبه 11n کافی ست اعداد سطر n+1ام مثلث خیام پاسکال را کنار هم بنویسیم.
![]() تمرین 2: با استفاده از مثلث خیام پاسکال حاصل 116 را به دست آورید. ابتدا بگویید از کدام سطر باید استفاده کنید؟
تمرین 2: با استفاده از مثلث خیام پاسکال حاصل 116 را به دست آورید. ابتدا بگویید از کدام سطر باید استفاده کنید؟
پاسخ: برای محاسبه 116 باید اعداد سطر هفتم را کنار هم بنویسیم.
1771561=116
کاربرد چهارم:
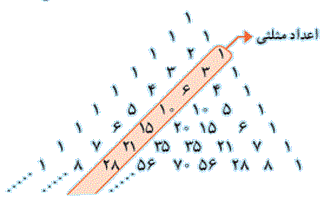
یکی دیگر از کاربردهای این مثلث که در کتاب ریاضی دهم برای به وجود آمدن اعداد مثلثی در قطر مثلث خیام پاسکال میباشد.
عددهای مثلثی همواره از 1 شروع میشوند و در مرحلهی اول 2 واحد به عدد اول اضافه میشود تا عدد دوم به دست آید. در مرحله بعد، 3 واحد به عدد قبلی اضافه میگردد و به این ترتیب الگوی عددی شکل میگیرد. در واقع اولین عدد مثلثی مساوی است با مجموع یک عدد از اعداد طبیعی، دومین معادل است با مجموع دو عدد از اعداد طبیعی، سومین معادل است با مجموع سه عدد از اعداد طبیعی و ... که بالاخره nامین عدد مثلثی معادل است با مجموع n عدد از اعداد طبیعی که مقدار این عدد معادل n(n+1)/2 خواهد بود.
... , ۲۱ , ۱۵ , ۱۰ , ۶ , ۳ , ۱
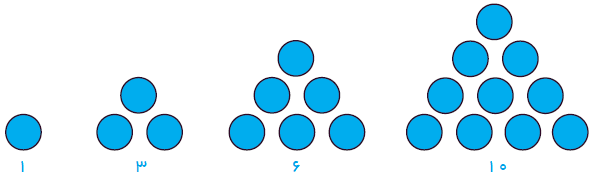
اعداد مثلثی به ترتیب بر روی سطر مورب از سمت چپ یا راست قرار دارد.
کاربرد پنجم:
ستون چهارم اعدادتترائدرال (tetrahedral) یا هرم مثلثالقاعده را میسازند:
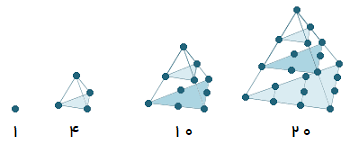
کاربرد ششم:
و بالاخره اینکه مجموع اعداد قطری، دنباله معروف فیبوناچی را خواهد ساخت. البته اگر مثلث را به شکل ویژه قائمالزاویه رسم کنیم:
مثلث سرپینسکی
تمام اعداد زوج را در «مثلث خیام – پاسکال» پاک کنید، آن چه باقی میماند «مثلث سرپینسکی» نام دارد:

مثلث سرپینسكی حاوی كپیهایی كوچكتر از خود است و میدانیم فراکتال شکل هندسی چند جزئی است که میتوان آن را به قسمتهایی تقسیم کرد، به طوری که هر قسمت یک کپی از "کل" شکل باشد.
بنابراین مثلث سرپینسکی نیز یک نوع فراکتال است که از مثلث خیام پاسکال براحتی میتواند حاصل شود.

گردآورنده: دنیاها، دانشنامۀ فارسی | www.donyaha.ir
![]()