توضیحات: نوشته شده توسط پیمان گلابی; دسته: فرمول های ریاضی; منتشر شده در 07 اسفند 1399; بازدید: 2364

اثبات فرمول های مثلثات

قانون جمع مربع سینوس و کسینوس

رابطه فیثاغورس را برای نسبت‌های مثلثاتی اثبات می‌کنیم. رابطه فیثاغورس به صورت زیر است:

$sin^{2}x + cos^{2}x = 1$ برای اثبات این رابطه به مفهوم سینوس و کسینوس رجوع می‌کنیم. مثلث زیر را در نظر بگیرید.

$اثبات فرمول های مثلثات$ در این مثلث طبق مفهوم سینوس و کسینوس و رابطه فیثاغورث داریم:

$\left.\begin{matrix}AC^{2}+BC^{2}=AB^{2}\\ sin \alpha = \frac{AC}{AB} \rightarrow AC=ABsin\alpha \\cos\alpha = \frac{BC}{AB} \rightarrow BC=ABcos\alpha\end{matrix}\right\} \rightarrow$

$\rightarrow (ABsin\alpha)^{2}+(ABcos\alpha)^{2}=AB \rightarrow AB^{2}(sin^{2}\alpha +cos^{2}\alpha)=AB^{2} \rightarrow sin^{2}\alpha +cos^{2} \alpha = 1$

قانون زاویه های متمم

2- ثابت کنید اگر $\alpha$ و $\beta$ متمم باشند، آنگاه: $sin\alpha=cos\beta$ و $cos\alpha=sin\beta$ برای این اثبات هم به تعریف سینوس و کسینوس در مثلث قائم‌الزاویه برمی‌گردیم. دو زاویه متمم را می‌توان دو زاویه غیرقائمه یک مثلث قائم الزاویه در نظر گرفت. زیرا در این صورت، مجموع زوایا برابر ۱۸۰ درجه خواهد شد. مثلث زیر را در نظر بگیرید:

$اثبات تمام فرمول های مثلثات$ در این مثلث، دو زاویه $\alpha$ و $\beta$ خود‌به‌خود متمم هستند. طبق تعریف سینوس و کسینوس داریم:

$\left.\begin{matrix}sin\alpha = \frac{AC}{AB}\\cos\beta=\frac{AC}{AB}\end{matrix}\right\} \rightarrow sin\alpha=cos\beta$

قانون تانژانت

ثابت کنید که $tan\theta = \frac{sec\theta}{csc\theta}$ از سمت راست معادله شروع می‌کنیم.

$\frac{sec\theta}{csc\theta}=\frac{\frac{1}{cos\theta}}{\frac{1}{sin\theta}} = \frac{sin\theta}{cos\theta} = tan\theta$

قانون رابطه تانژانت و کتانژانت با سینوس و کسینوس

ثابت کنید $1+tan^{2}\theta = sec^{2}\theta &S=2$ و $1+cot^{2}\theta=csc^{2}\theta$ از رابطه فیثاغورث (رابطه 1) در این اثبات کمک می‌گیریم.

$1+tan^{2}\theta = 1+\frac{sin^{2}\theta}{cos^{2}\theta} = \frac{cos^{2}\theta+sin^{2}\theta}{cos^{2}\theta} = \frac{1}{cos^{2}\theta} = sec^{2}\theta$

$1+cot^{2}\theta = 1+\frac{cos^{2}\theta}{sin^{2}\theta} = \frac{sin^{2}\theta+cos^{2}\theta}{sin^{2}\theta} = \frac{1}{sin^{2}\theta} = csc^{2}\theta$

سینوس جمع دو زاویه

قانون سینوس جمع دو زاویه را اثبات می‌کنیم.

$sin(\alpha+\beta)=sin\alpha cos\beta + cos\alpha sin\beta$

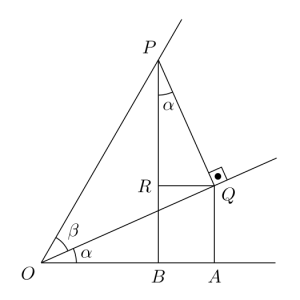
برای اثبات این قانون مجددا باید به مفهوم، سینوس و کسینوس رجوع کنیم. شکل زیر را در نظر داشته باشید و اثبات را مرحله به مرحله دنبال کنید. در هر مرحله، نگاهی هم به شکل زیر بیاندازید.

$نحوه اثبات روابط مثلثاتی$

مرحله 1: زاویه $\alpha$ و $\beta$ را به صورت مجاور رسم می‌کنیم. یعنی به صورتی که یک ضلع‌شان مشترک باشد.
مرحله 2: نقطه $P$ را روی ضلع زاویه دوم در نظر می‌گیریم. فاصله نقطه $P$ تا نقطه $O$ برابر یک است.
مرحله 3: خط $PQ$ را طوری رسم می‌کنیم که بر ضلع مشترک دو زاویه عمود باشد. در این صورت، مثلث $POQ &S=2$ یک مثلث قائم‌الزاویه خواهد بود.
مرحله 4: از نقطه $P$ و $Q$ دو خط بر ضلع غیرمجاور زاویه $\alpha$ عمود می‌کنیم. این دو خط، ضلع را در نقاط $A$ و $B$ قطع می‌کنند. دو مثلث $OAQ$ و $OBP$ قائم‌الزاویه هستند.
مرحله 5: از نقطه Q خطی موازی با AB رسم می‌کنیم.
مرحله 6: حال داریم $RPQ = \alpha$ . به دلیل خاصیت دو خط موازی و یک خط متقاطع. خط $QR$ موازی $OA$ است.
مرحله 7: با توجه به آنچه تا به حال گفته شد، داریم:

$\left.\begin{matrix}sin\beta=\frac{PQ}{OP}\\cos\beta=\frac{OQ}{OP} \\OP=1 \end{matrix}\right\} \rightarrow \left\{\begin{matrix}sin\beta=PQ\\ cos\beta=OQ\end{matrix}\right.$

$\left.\begin{matrix}sin\alpha=\frac{AQ}{OQ} \rightarrow AQ=sin\alpha OQ\\ OQ = cos\beta\end{matrix}\right\} \rightarrow AQ=sin\alpha cos\beta$

$\left.\begin{matrix}cos\alpha=\frac{PR}{PQ} \rightarrow PR=cos\alpha PQ\\ PQ = sin\beta\end{matrix}\right\} \rightarrow PR=sin\beta cos\alpha$

حال با توجه به این اطلاعات، $sin(\alpha + \beta)$ را حساب می‌کنیم.

$sin(\alpha + \beta) = \frac{PB}{PO} = PB = PR+RB = AQ+PR = sin\alpha cos\beta + cos\alpha sin\beta$

کسینوس جمع دو زاویه

قانون کسینوس جمع دو زاویه را اثبات می‌کنیم. درست مطابق روش سینوس عمل می‌کنیم. مثلث شکل بالا را ببینید و روابط زیر را با آن تطبیق دهید.

$\left.\begin{matrix} OP=1\\ PQ = sin\beta \\OQ=cos\beta \\cos \alpha = \frac{OA}{OQ} \\ sin \alpha = \frac{RQ}{PQ} \end{matrix}\right\} \rightarrow \left\{\begin{matrix} OA=cos\alpha cos\beta\\ RQ=sin\alpha \sin\beta \end{matrix}\right.$

$cos(\alpha + \beta) = OB = OA-AB = cos\alpha cos\beta - sin\alpha sin\beta$

سینوس و کسینوس تفریق دو زاویه

قوانین تفریق دو زاویه را برای سینوس و کسینوس اثبات می‌کنیم. وقتی قوانین جمع دو زاویه را داشته باشیم، با منفی کردن یکی از زوایا، قوانین تفریق هم به دست می‌آید.

$sin(\alpha - \beta) = sin(\alpha)cos(-\beta)+cos(\alpha)sin(-\beta)$

می‌دانیم که سینوس تابعی فرد و کسینوس تابعی زوج است. پس داریم:

$sin(\alpha)cos(-\beta)+cos(\alpha)sin(-\beta) = sin(\alpha)cos(\beta)-cos(\alpha)sin(\beta)$

$cos(\alpha-\beta) = cos(\alpha)cos(-\beta)-sin(\alpha)sin(-\beta) = cos(\alpha)cos(\beta)+sin(\alpha)sin(\beta)$

تانژانت و کتانژانت جمع دو زاویه

ثابت کنید که قوانین زیر برای تانژانت و کتانژانت جمع دو زاویه برقرارند.

$tan(\alpha + \beta) = \frac{tan\alpha + tan\beta}{1-tan\alpha tan\beta}$

$cot(\alpha + \beta) = \frac{cot\alpha cot\beta -1}{cot\alpha + cot\beta}$

با توجه به اتحادهای مثلثاتی 5 و 6 که سینوس و کسینوس جمع دو زاویه را بیان می‌کنند، داریم:

$tan(\alpha+\beta) = \frac{sin(\alpha + \beta)}{cos(\alpha + \beta)} = \frac{sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)}{cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)}$

صورت و مخرج سمت راست معادله را بر $cos\alpha cos\beta$ تقسیم می‌کنیم.

$\frac{\frac{ sin(\alpha)cos(\beta)+cos(\alpha)sin(\beta)}{ cos\alpha cos\beta }}{\frac{ cos(\alpha)cos(\beta)-sin(\alpha)sin(\beta)}{ cos\alpha cos\beta }} = \frac{tan\alpha + tan\beta}{1-tan\alpha tan\beta}$

برای کتانژانت مجموع دو زاویه هم داریم:

$cot(\alpha + \beta) = \frac{cos(\alpha + \beta)}{sin(\alpha + \beta)} = \frac{cos\alpha cos\beta - sin\alpha sin\beta}{sin\alpha cos\beta + cos\alpha sin\beta} = \frac{\frac{ cos\alpha cos\beta - sin\alpha sin\beta }{sin\alpha sin\beta}}{\frac{ sin\alpha cos\beta + cos\alpha sin\beta }{sin\alpha sin\beta}} = \frac{cot\alpha cot\beta -1}{cot\alpha + cot\beta}$

سینوس و کسینوس دو برابر زاویه

اثبات می‌کنیم که فرمول زاویه دوبرابر برای سینوس و کسینوس به صورت زیر است:

$sin 2\alpha = 2sin\alpha cos\alpha$

$cos 2\alpha = cos^{2}\alpha-sin^{2}\alpha$

برای اثبات این دو رابطه، کافیست در فرمول‌های مربوط به سینوس و کسینوس مجموع دو زاویه، به جای زاویه بتا، زاویه آلفا قرار دهیم.

$sin2\alpha = sin(\alpha + \alpha)=sin\alpha cos\alpha + cos\alpha sin\alpha = 2sin\alpha cos\alpha$

$cos2\alpha = cos(\alpha + \alpha) = cos\alpha cos\alpha - sin\alpha sin\alpha = cos^{2}\alpha - sin^{2}\alpha$

سینوس و کسینوس سه برابر زاویه

نشان دهید که فرمول زاویه سه برابر برای سینوس و کسینوس به صورت زیر است:

$sin3x = 3sinx - 4sin^{3}x$

$cos3x = 4cos^{3}x - 3cosx$

طبق فرمول‌های سینوس و کسینوس مجموع دو زاویه داریم:

$sin3x = sin(2x+x) = sin2x cosx + cos2x sinx = 2sinx cosx cosx + (cos^{2}x-sin^{2}x)sinx = 2sinx cos^{2}x + cos^{2}xsinx-sin^{3}x$

حال از رابطه فیثاغورس کمک می‌گیریم.

$2sinx cos^{2}x + cos^{2}xsinx-sin^{3}x = 2sinx(1-sin^{2}x)+(1-sin^{2}x)sinx-sin^{3}x = 2sinx-2sin^{3}x+sinx-sin^{3}x-sin^{3}x=3sinx-4sin^{3}x$

برای کسینوس هم به همین صورت از کسینوس مجموع و فیثاغورث استفاده می‌کنیم.

$cos3x = cos(2x+x) = cos2x cosx - sin2x sinx = (cos^{2}x-sin^{2}x)cosx -2sinx cosx sinx = cos^{3}x-cosx sin^{2}x -2cosx sin^{2}x = cos^{3}x-cosx(1-cos^{2}x)-2cosx(1-cos^{2}x) = cos^{3}x-cosx+cos^{3}x-2cosx+2cos^{3}x = 4cos^{3}x-3cosx$

تانژانت نصف زاویه

ثابت کنید که رابطه زیر برای تانژانت نصف زاویه برقرار است.

$tan(\frac{x}{2}) = \frac{sinx}{1+cosx}$

ابتدا فرمول سینوس و کسینوس نصف زاویه را به دست می‌آوریم تا با تقسیم آنها، فرمول تانژانت نصف زاویه هم به دست بیاید. برای اینکار از فرمول سینوس دو برابر زاویه کمک می‌گیریم.

$cosx = cos(2\frac{x}{2})= cos^{2}(\frac{x}{2}) - sin^{2}(\frac{x}{2}) \rightarrow \left\{\begin{matrix}sin(\frac{x}{2})=\pm \sqrt{\frac{1-cosx}{2}}\\ cos(\frac{x}{2})=\pm \sqrt{\frac{1+cos}{2}}\end{matrix}\right.$

پس داریم:

$tan(\frac{x}{2})=\frac{sin(\frac{x}{2})}{cos(\frac{x}{2})} = \frac{\sqrt{\frac{1-cosx}{2}}}{\sqrt{\frac{1+cosx}{2}}} = \sqrt{\frac{1-cosx}{1+cosx}}$

صورت و مخرج عبارت بالا را در $1+cosx$ ضرب می‌کنیم.

$tan(\frac{x}{2}) = \sqrt{\frac{(1-cosx)(1+cosx)}{(1+cosx)(1+cosx)}} = \sqrt{\frac{1-cos^{2}x}{(1+cosx)^{2}}} = \sqrt{\frac{sin^{2}x}{(1+cosx)^{2}}} = \frac{sinx}{1+cosx}$

اگر به جای $1+cos$ صورت مخرج را در $1-cosx$ ضرب کنیم خواهیم داشت:

$tan(\frac{x}{2}) = \frac{1-cosx}{sinx}$

تبدیل جمع به ضرب سینوس و کسینوس

رابطه تبدیل جمع به ضرب را برای سینوس و کسینوس اثبات می‌کنیم.

$sinx + siny = 2sin(\frac{x+y}{2})cos(\frac{x-y}{2})$

$cosx + cosy = 2cos(\frac{x+y}{2})cos(\frac{x-y}{2})$

برای اثبات این روابط از قانون سینوس و کسینو مجموع و تفاضل دو زاویه کمک می‌گیریم. ابتدا فرمول سینوس جمع دو زاویه سینوس تفاضل را می‌نویسیم و سپس طرفین این دو رابطه را به هم جمع می‌کنیم.

$\left.\begin{matrix} sin(x+y)=sinx cosy + cosx siny \\ sin(x-y)= sinx cosy - cosx siny \end{matrix}\right\} \rightarrow$

$\rightarrow sin(x+y) + sin(x-y) = 2sinxcosy$

حال قرار می‌دهیم $x+y = \alpha$ و $x-y=\beta$ . پس داریم:

$sin\alpha + sin\beta = 2sin(\frac{\alpha + \beta}{2})cos(\frac{\alpha - \beta}{2})$

برای اثبات تبدیل جمع به ضرب سینوس هم به همین صورت عمل می‌کنیم.

$\left.\begin{matrix} cos(x+y)=cosx cosy - sinx siny \\ cos(x-y)= cosx cosy + sinx siny \end{matrix}\right\} \rightarrow$

$cos(x+y) + cos(x-y) = 2cosxcosy$

درست مثل اثبات قبل، قرار می‌دهیم: $x+y = \alpha$ و $x-y=\beta$ و داریم:

$cos(\alpha)+cos(\beta)=2cos(\frac{\alpha + \beta}{2})cos(\frac{\alpha-\beta}{2})$

اگر بخواهیم که $sinx - siny$ و $cosx - cosy$ را هم اثبات کنیم، کافیست وقتی روابط جمع و تفاضل دو زاویه را می‌نویسیم، طرفین دو معادله را به جای جمع، از هم کم کنیم. باقی اثبات مشابه است.