آندری آندریویچ مارکوف ریاضیدانی روسی بود که بیشتر به دلیل کارش در مورد فرآیندهای تصادفی (کاتورهای) شناخته شده است. موضوع اصلی تحقیقات او بعداً به عنوان زنجیره مارکوف شناخته شد. او همچنین یک شطرنج باز قوی بود. از زنجیره مارکوف در بسیاری از علوم از جمله فیزیک، اقتصاد، آمار، زیستشناسی استفاده میشود و مسائلی مانند حرکت براونی، گام تصادفی (ولگشت) و پیجرنک (PageRank) از مشهورترین موارد کاربردهای زنجیره مارکوف هستند.
مارکوف در ابتدا تمرکز را روی نظریه اعداد میگذاشت. ولی بعداً توجهاش به «نظریه احتمالات» جلب شد و بعد از بازنشستگی و تا آخر عمر مشغول به تدریس بود. از دستاوردهای وی تدوین قانون اعداد بزرگ و قضیه حد مرکزی جهت کاربرد در دنبالههای معینی از متغیرهای تصادفی وابسته بود که بعدها به عنوان زنجیره مارکوف شناخته شد.
زندگی
آندری مارکوف در ژوئن ۱۸۵۶ در روسیه دیده به جهان گشود. او فارغ التحصیل دانشگاه سنت پترزبورگ در سال ۱۸۷۸ بود. او در رشته دانشگاهی خود در بسیاری از موضوعات به جز ریاضیات خیلی ضعیف عمل کرد. او تحصیلاتش را در دانشگاه به پایان رساند و بعدها از او درخواست شد به عنوان یک ریاضیدان مشغول به کار شود. بعدها در دبیرستان تدریس کرد و مطالعات ریاضی خود را ادامه داد. در این زمان برای مهارتهای ریاضی خود یک کاربرد عملی پیدا کرد و به این نتیجه رسید که میتواند از زنجیر برای مدلسازی حروف صدادار و بیصدا در ادبیات روسی استفاده کند. وی در سال ۱۸۸۶ مدرک پروفسوری خود را دریافت کرد.
کارهای زود هنگام مارکوف در نظریه اعداد، آنالیز، حدود انتگرالها، همگرایی سریها، دنباله کسرها و ... بسیار اساسی بود. بعد از سال ۱۹۰۰، مارکوف تحت تأثیر استاد خود چبیشف، از روش دنبالههای کسرها در نظریه احتمالات استفاده کرد.
وی هم چنین در مورد رشتههای متغیرهای وابسته متقابل، مطالعاتی انجام داد. با امید ثابت کردن قوانین حدی در احتمالات در حالات کلی آنها، او قضیه حد مرکزی را با در نظر گرفتن فرضهای کامل آن، اثبات کرد. مارکوف به دلیل مطالعاتش پیرامون زنجیرهای مارکوف که رشتههایی از متغیرهای تصادفی هستند، معروف است. در زنجیرهای مارکوف، متغیر بعدی توسط متغیر کنونی مشخص می شود ولی از راهی که تا کنون طی شده است مستقل است.
زنجیره مارکوف
رویدادهای اقلیمی به عنوان پدیدههای تصادفی به طور دقیق قابل پیش بینی نیستند ولی از مشاهده پیاپی آنها آگاهیهای مفیدی بدست میآید که از طریق قوانین احتمالی قابل تعریف هستند. فهم بسیاری از رویدادهای اقلیمی منوط به شناخت احتمال وقوع این فرایندهاست براساس این قوانین احتمالاتی برخی پدیدههای تصادفی شانس بیشتری برای وقوع دارند. فرایندهای تصادفی به پدیدههایی گفته می شود که نتوان نتیجه آنها را پیش از رخ دادن به طور قطع معلوم کرد.
یک فرایند تصادفی مجموعهای از متغیرهای تصادفی که طی زمان، مقادیر (مشاهدات) مختلفی را نشان میدهد گفته میشود مثل وقوع بارش با مقدار معین ،خشکسالی و ترسالیها. برای محاسبه شانس وقوع پیشامدها لازم است مدل مناسبی انتخاب شود. بررسی این حالتهای نامعین یا تصادفی و انتخاب مدل را دانش احتمال برعهده دارد. آید .
اگر فرایند تصادفی [x(t) , t є T] به گونهای باشد که با معلوم بودن مقدار (x(s مقادیر (x(t برای s<t وابسته به مقادیر (x(u برای u<s نباشد ، آنگاه فر ایند را فرایند مارکوف گوییم که تعریف آن به این صورت بیان میشود که: فرایندهای تصادفی که با اطلاع از وضعیت کنونی ، وضعیتهای گذشته آنها اثری بر احتمالهای شرطی پیشامدهای که در آینده رخ میدهند، ندارد، فرایند مارکوف میگویند. به عبارتی به صورت زیر بیان می شود.
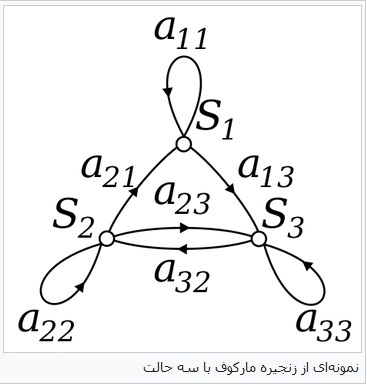
فرایند مارکوف را که فضایی وضعیت آن متناهی یا نا متناهی شماراست ، زنجیره مارکوف میگوییم. زنجیره مارکوف یک روش ریاضی برای مدلبندی فرایندهای تصادفی است. که توالی از مشاهدات را در طول زمان نشان میدهد. وابستگی این زنجیره به زمان یا از طریق ضرایب همبستگی و یا با استفاده از ماتریسهای احتمال انتقال بیان میشود. تجزیه و تحلیل زنجیره مارکوف راهحلی است برای تحلیل کنونی متغیرهای معلوم تا پیش بینی حرکات آینده متغیرها امکان پذیر باشد که در صورتی مارکوف مرتبه اول نتواند پاسخگوی احتمالات دقیق آینده باشد باید از درجه بالاتر این تحلیل استفاده شود.
هر برآمد (نتیجه) فرایندهای تصادفی که تنها به برآمد بلافاصله قبل از آن بستگی دارد را فرایند تصادفی با ویژگی مارکوف میگویند. براین اساس فرایند تصادفی که در ویژگی مارکوف صدق میکند فرایند یا زنجیرههای مارکوف می گویند. زنجیره گویایی این واقعیت است که هر برآمد به رویداد بلافاصله قبل از خودش وابسته میباشد و به رویدادهای ماقبل خودش مربوط نمیباشد در واقع در این رویه احتمال وقوع یک حالت اقلیمی در زمان t به وضعیت آن در زمان قبل یعنی t-1 بستگی دارد . برای مثال روز خشک امروز بر اساس وضعیت تر روز قبل بررسی میشود ، بنابراین برای هر زوج حالتهای متوالی یک احتمال وجود دارد در این صورت احتمال تغییر هریک از مشاهدات از حالتی به حالت دیگر مشخص میشود. زنجیره مارکوف همچنین احتمال اینکه یک رویداد از چه تداومی تبعیت میکند را مورد بحث قرار میدهد. به عنوان مثال احتمال اینکه یک ترسالی با چند مرحله تغییر بعد از یک دوره نرمال بارش رخ میدهد یک فرایند مارکوفی است.
در سال ۱۹۲۳ «نوربرت واینر» اولین کسی بود که پیرامون یک سلسله از این مراحل مارکوف شروع به بحثی جدی کرد. اساس یک نظریه اصلی در سال ۱۹۳۰ توسط کولموگروف فراهم شد.
علایق دیگر
مارکوف به شاعری هم علاقه مند بود و پیرامون ساختار شعری مطالعاتی انجام داد. جالب اینکه کولموگروف هم، چنین علایقی داشت. مارکوف پسری به اسم خودش داشت که در ۹ سپتامبر ۱۹۰۳ به دنیا آمد و راه پدرش را ادامه داد.
افتخارات
در سال ۱۸۷۷ مدال طلا برای راهحل برجسته حل مسئله به وی اهدا شد. سال بعد در آزمونهای نامزدی برای استادی قبول شد و در دانشگاه ماند تا برای سمت استادیاری آماده شود. در آوریل ۱۸۸۰، مارکوف از رساله فوق لیسانسش در «اشکال مربع دودویی با تعریف مثبت» دفاع کرد که مورد تشویق قرار گرفت. چهار سال بعد در سال ۱۸۸۴، از تز دکترای خود با عنوان «کاربرد خاص جبری بخش متوالی» دفاع کرد.

شغل استادی او پس از دفاع از پایاننامه کارشناسیارشد در پاییز سال ۱۸۸۰ آغاز شد. وی در زمینه دیفرانسیل و انتگرال به تدریس پرداخت. بعدها بهطور متناوب دربارهٔ «معرفی تحلیل»، نظریه احتمال و ریاضیات تفاوتها تدریس کرد. از ۱۸۹۵ تا ۱۹۰۵ نیز محاسبات دیفرانسیل را تدریس کرد.
مارکوف و برادر کوچکترش، ولادیمیر، نابرابری برادران مارکوف را ثابت کردند. پسرش آندری مارکوف کوچک (۱۹۰۳–۱۹۷۹) نیز یک ریاضیدان برجسته بود که به برساختگی و نظریه توابع بازگشتی کمک میکرد.
مرگ او
این دانشمند بزرگ در ۲۰ جولای سال ۱۹۲۲ در سنت پترزبورگ روسیه چشم از جهان فرو بست.
گردآورنده : دنیاها،دانشنامهٔ فارسی | www.donyaha.ir